
 如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且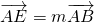 ,
,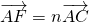 ,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则
,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则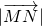 的最小值为________.
的最小值为________.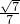

 =-
=- .连接AM、AN,利用三角形中线的性质,得到
.连接AM、AN,利用三角形中线的性质,得到 =
= (
( )且
)且 =
= (
( +
+ ),进而得到
),进而得到 =
= -
- =
= (1-m)
(1-m) +
+ (1-n)
(1-n) .将此式平方,代入题中数据化简可得
.将此式平方,代入题中数据化简可得 =
= (1-m)2-
(1-m)2- (1-m)(1-n)+
(1-m)(1-n)+ (1-n)2,结合m+4n=1消去m,得
(1-n)2,结合m+4n=1消去m,得 =
= n2-
n2- n+
n+ ,结合二次函数的性质可得当n=
,结合二次函数的性质可得当n= 时,
时, 的最小值为
的最小值为 ,所以
,所以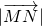 的最小值为
的最小值为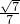 .
. 解:连接AM、AN,
解:连接AM、AN,
 =|
=| |•|
|•| |cos120°=-
|cos120°=-
 =
= (
( )=
)= (
(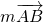 +
+ )
) =
= (
( +
+ ),
), =
= -
- =
= (1-m)
(1-m) +
+ (1-n)
(1-n)
 =[
=[ (1-m)
(1-m) +
+ (1-n)
(1-n) ]2=
]2= (1-m)2+
(1-m)2+ (1-m)(1-n)
(1-m)(1-n) •
• +
+ (1-n)2
(1-n)2 (1-m)2-
(1-m)2- (1-m)(1-n)+
(1-m)(1-n)+ (1-n)2,
(1-n)2, =
= ×(4n)2-
×(4n)2- ×4n(1-n)+
×4n(1-n)+ (1-n)2=
(1-n)2= n2-
n2- n+
n+
 时,
时, 的最小值为
的最小值为 ,此时
,此时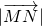 的最小值为
的最小值为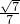 .
.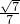
 模的最小值,着重考查了平面向量数量积公式及其运算性质和二次函数的最值求法等知识,属于中档题.
模的最小值,着重考查了平面向量数量积公式及其运算性质和二次函数的最值求法等知识,属于中档题. 

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
 (2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
(2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且| AE |
| AB |
| AF |
| AC |
| MN |
| ||
| 7 |
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三高考模拟卷(二)理科数学试卷(解析版) 题型:解答题
如图,在三棱锥A-BCD中,△ABD和△BCD是两个全等的等腰直角三角形,O为BD的中点,且AB=AD=CB=CD=2,AC= .
.
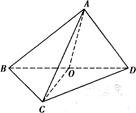
(1)当 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD;
(2)当二面角 的大小为
的大小为 时,求二面角
时,求二面角 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源:2013年江苏省苏北三市高考数学一模试卷(宿迁、徐州、淮安)(解析版) 题型:填空题
 如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且 ,
, ,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则
,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则 的最小值为 .
的最小值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com