答案:
解析:
|
(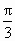 ,π) ,π)
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在极坐标系中,若等边三角形ABC(顶点A,B,C按顺时针方向排列)的顶点A,B的极坐标分别为 ,则顶点C的极坐标为________; ,则顶点C的极坐标为________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知长方体ABCD-A1B1C1D1的外接球的表面积为16π,则该长方体的表面积的最大值为
|
| [ ] |
A. |
32
|
B. |
36
|
C. |
48
|
D. |
64
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知α∈( ,π),sinα= ,π),sinα= ,则tan(α+ ,则tan(α+ )等于 )等于
|
| [ ] |
A. |
-7
|
B. |
7
|
C. |
-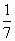
|
D. |
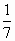
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
关于函数函数f(x)=2cosx(cosx+ sinx)-1,以下结论正确的是 sinx)-1,以下结论正确的是
|
| [ ] |
A. |
f(x)的最小正周期是π,在区间(- , , )是增函数 )是增函数
|
B. |
f(x)的最小正周期是π,在区间(- , , )是增函数 )是增函数
|
C. |
f(x)的最小正周期是π,最大值是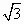
|
D. |
f(x)的最小正周期是2π,最大值是2
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知椭圆 + + =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F. ,倾斜角为45°的直线l过点F.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为F1,问抛物线y2=4x上是否存在一点M,使得M与F1关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知α∈( ,π),sinα= ,π),sinα= ,则tan(α+ ,则tan(α+ )等于 )等于
|
| [ ] |
A. |
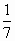
|
B. |
7
|
C. |
-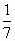
|
D. |
-7
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知椭圆 + + =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F. ,倾斜角为45°的直线l过点F.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为F1,问抛物线y2=4x上是否存在一点M,使得M与F1关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由.
|
|
|
查看答案和解析>>
