
分析 (1)求出l1、l2之间的距离,设直线m与l1所成锐角为θ,求解θ=30°,推出直线m的倾斜角为90°或30°,然后求解直线方程.
(2)求出直线n的斜率是$k=-\frac{{\sqrt{3}}}{3}$,设直线n的方程为$y=-\frac{{\sqrt{3}}}{3}x+b$,利用三角形的面积求解即可.
解答 (1)解:l1、l2之间的距离$d=\frac{|3-1|}{{\sqrt{{{(\sqrt{3})}^2}+{{(-1)}^2}}}}=1$,
设直线m与l1所成锐角为θ,则$sinθ=\frac{1}{2}$,∴θ=30°,
直线m的倾斜角为90°或30° 所以,直线m的方程为$x=\sqrt{3}$或$y-4=\frac{{\sqrt{3}}}{3}(x-\sqrt{3})$
即$x=\sqrt{3}$或$y=\frac{{\sqrt{3}}}{3}x+3$.
(2)解:直线l1的斜率是${k_1}=\sqrt{3}$,
∵n⊥l,∴直线n的斜率是$k=-\frac{{\sqrt{3}}}{3}$
设直线n的方程为$y=-\frac{{\sqrt{3}}}{3}x+b$,令y=0得$x=\sqrt{3}b$,令x=0得y=b
∴$\frac{1}{2}|\sqrt{3}b|•|b|=2\sqrt{3}$,∴b=±2,
∴直线n的方程为$y=-\frac{{\sqrt{3}}}{3}x+2$或$y=-\frac{{\sqrt{3}}}{3}x-2$.
点评 本题考查直线方程的求法,直线的倾斜角截距式方程的应用,考查计算能力.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或3 | B. | 5 | C. | 3或5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
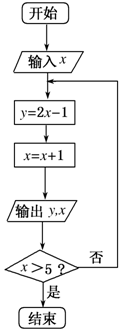 如图所示,已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},全集U=Z.当x=-1时,(∁UA)∩B={-3,-1,7,9}.
如图所示,已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},全集U=Z.当x=-1时,(∁UA)∩B={-3,-1,7,9}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com