
分析 利用函数微分的公式,即可求得函数的微分.
解答 解:(1)dx=$\sqrt{1+(y′)^{2}}$dx,
而y=ln(1-x2);
∴y′=$\frac{-2x}{1-{x}^{2}}$,
故ds=$\sqrt{1+\frac{4{x}^{2}}{(1-{x}^{2})^{2}}}$dx=$\frac{1+{x}^{2}}{1-{x}^{2}}$dx,
(2)ds=$\sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2}}$dt,
而)$\left\{\begin{array}{l}{x=a•cost}\\{y=b•sint}\end{array}\right.$,
∴$\frac{dx}{dt}$=-asint,
$\frac{dy}{dt}$=bcost,
故ds=$\sqrt{{a}^{2}si{n}^{2}t+{b}^{2}co{s}^{2}t}$dt,
(3)ds=$\sqrt{r{′}^{2}(θ)+{r}^{2}(θ)}$dθ,
而r=a•θ,r′=a,
故ds=$\sqrt{{a}^{2}+{a}^{2}{θ}^{2}}$dθ=a$\sqrt{1+{θ}^{2}}$dθ
点评 本题主要考察弧微公式和微积分基本定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
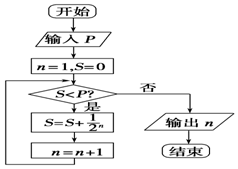
| A. | $\frac{7}{8}$<P≤$\frac{15}{16}$ | B. | P>$\frac{15}{16}$ | C. | $\frac{3}{4}$<P≤$\frac{7}{8}$ | D. | $\frac{7}{8}$≤P<$\frac{15}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com