
分析 先设x+y=a,得到$\frac{1}{a}$(x+y)=1,从而有x+y+$\frac{1}{x}$+$\frac{9}{y}$=a+$\frac{16}{a}$,进而得到不等式10≥a+$\frac{16}{a}$,解出即可.
解答 解:设x+y=a,显然a>0,
则$\frac{1}{a}$(x+y)=1,
∴x+y+$\frac{1}{x}$+$\frac{9}{y}$
=a+$\frac{1}{a}$(x+y)($\frac{1}{x}$+$\frac{9}{y}$)
=a+$\frac{10}{a}$+$\frac{1}{a}$•2$\sqrt{\frac{9x}{y}•\frac{y}{x}}$
=a+$\frac{16}{a}$,
当且仅当3x=y时“=”成立,
∴10≥a+$\frac{16}{a}$,
∴a2-10a+16≤0,
解得:2≤a≤8.
∴(x+y)min=2.
点评 本题考查了基本不等式的性质,设x+y=a,得到$\frac{1}{a}$(x+y)=1是解题的关键,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
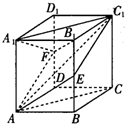 如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com