
分析 (1)利用两角和与差的余弦公式展开,结合二倍角公式和辅助角公式进行化简,则函数f(x)的对称中心及在[-$\frac{π}{4}$,$\frac{π}{4}$]的取值范围可求;
(2)由f(A)=-$\frac{1}{2}$,结合(1)求出A=$\frac{π}{4}$,再由三角形的面积求出c,代入余弦定理求得a,则$\frac{a+b}{sinA+sinB}$=$\frac{a}{sinA}$可求.
解答 解:(1)f(x)=cos($\frac{π}{3}$+x)cos($\frac{π}{3}$-x)-sinxcosx+$\frac{1}{4}$
=$(cos\frac{π}{3}cosx-sin\frac{π}{3}sinx)(cos\frac{π}{3}cosx+sin\frac{π}{3}sinx)$$-\frac{1}{2}sin2x+\frac{1}{4}$
=$(\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx)(\frac{1}{2}cosx+\frac{\sqrt{3}}{2}sinx)-\frac{1}{2}sin2x+\frac{1}{4}$
=$\frac{1}{4}co{s}^{2}x-\frac{3}{4}si{n}^{2}x-\frac{1}{2}sin2x+\frac{1}{4}$
=$\frac{1}{4}(co{s}^{2}x-si{n}^{2}x)-\frac{1}{2}si{n}^{2}x-\frac{1}{2}sin2x+\frac{1}{4}$
=$\frac{1}{4}cos2x-\frac{1}{2}•\frac{1-cos2x}{2}-\frac{1}{2}sin2x+\frac{1}{4}$
=$-\frac{1}{2}(sin2x-cos2x)$
=$-\frac{\sqrt{2}}{2}sin(2x-\frac{π}{4})$.
由$2x-\frac{π}{4}=kπ$,得$x=\frac{kπ}{2}+\frac{π}{8},k∈Z$.
∴函数f(x)的对称中心为($\frac{kπ}{2}+\frac{π}{8},0$),k∈Z.
∵-$\frac{π}{4}$≤x≤$\frac{π}{4}$,∴$-\frac{π}{2}≤2x≤\frac{π}{2}$,则$-\frac{3π}{4}≤2x-\frac{π}{4}≤0$,
则f(x)在[-$\frac{π}{4}$,$\frac{π}{4}$]的取值范围为[0,$\frac{\sqrt{2}}{2}$];
(2)由f(A)=-$\frac{1}{2}$,得$-\frac{\sqrt{2}}{2}sin(2A-\frac{π}{4})=-\frac{1}{2}$,
∴$sin(2A-\frac{π}{4})=\frac{\sqrt{2}}{2}$.
∵$-\frac{π}{4}<2A-\frac{π}{4}<\frac{7π}{4}$,
∴$2A-\frac{π}{4}$=$\frac{π}{4}$或$2A-\frac{π}{4}$=$\frac{3π}{4}$,
则A=$\frac{π}{4}$或A=$\frac{π}{2}$.
又△ABC为非直角三角形,∴A=$\frac{π}{4}$.
∵b=1,
∴S△ABC=$\frac{1}{2}bc•sinA=\frac{1}{2}c•sin\frac{π}{4}=\frac{\sqrt{2}}{4}c=2$,得$c=4\sqrt{2}$.
∴${a}^{2}={b}^{2}+{c}^{2}-2bc•cosA=1+32-8\sqrt{2}×\frac{\sqrt{2}}{2}$=25.
∴a=5.
则$\frac{a+b}{sinA+sinB}$=$\frac{a}{sinA}=\frac{5}{sin\frac{π}{4}}=\frac{5}{\frac{\sqrt{2}}{2}}=5\sqrt{2}$.
点评 本题给出三角函数表达式,求函数的对称中心及值域,考查了三角形的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
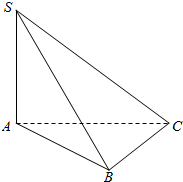 如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )| A. | $\frac{3a}{2}$ | B. | $\frac{2\sqrt{21}}{7}$a | C. | $\frac{5a}{2}$ | D. | $\frac{7a}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
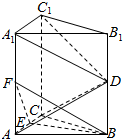 在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC
在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
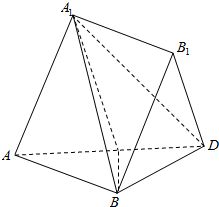 如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.
如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{9}{16}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com