
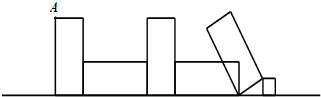
分析 由弧长公式计算各段弧长,相加可得答案.
解答 解:第一次是以B为旋转中心,以BA=$\sqrt{{2}^{2}+1}=\sqrt{5}$为半径旋转90°,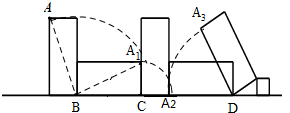
此次点A走过的路径是$\frac{π}{2}×\sqrt{5}=\frac{\sqrt{5}}{2}π$.
第二次是以C为旋转中心,
以CA1=1为半径旋转90°,
此次点A走过的路径是$\frac{π}{2}×1$=$\frac{π}{2}$.
第三次是以D为旋转中心,
以DA2=2为半径旋转60°,
此次点A走过的路径是$\frac{π}{3}×2=\frac{2}{3}π$,
∴点A三次共走过的路径是$\frac{\sqrt{5}π}{2}+\frac{π}{2}+\frac{2π}{3}$=$\frac{7}{6}π+\frac{\sqrt{5}}{2}π$.
故答案为:$\frac{7}{6}π+\frac{\sqrt{5}}{2}π$.
点评 本题考查弧长公式,求出各段弧长的圆心角和半径是解决问题的关键,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{1-{m^2}}$ | B. | $\sqrt{1-{m^2}}$ | C. | $±\sqrt{{m^2}-1}$ | D. | $-\sqrt{1-{m^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
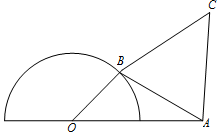 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
| y | 1.501 | 4.413 | 7.498 | 12.04 | 17.93 |
| A. | y=2x-1+1 | B. | $y=\frac{3}{2}{log_2}x$ | C. | $y=\frac{1}{2}{x^2}-\frac{1}{2}$ | D. | y=-2x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{3}$π | B. | $\frac{28}{3}$π | C. | $\frac{28\sqrt{21}}{27}$π | D. | $\frac{25\sqrt{21}}{27}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com