
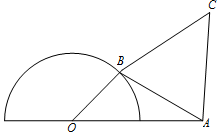
 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大? 分析 设∠AOB=θ,AB=x,则由余弦定理求得 x2=5-4cosθ.再利用两角和差的正弦公式化简SOACB =S△AOB+S△ABC 的解析式,从而求得SOACB的面积取得最大值.
解答 解:设∠AOB=θ,则SOACB =S△AOB+S△ABC.
设AB=x,则x2=OB2+OA2-2OB•OAcosθ=12+22-2×1×2•cosθ=5-4cosθ.
故 SOACB=S△AOB+S△ABC=$\frac{1}{2}$×1×2•sinθ+$\frac{1}{2}•x•x•sin\frac{π}{3}$
=sinθ+$\frac{\sqrt{3}}{4}$(5-4cosθ)=$\frac{5\sqrt{3}}{4}$+2sin(θ-$\frac{π}{3}$),
∴当sin(θ-$\frac{π}{3}$)=1,即θ=$\frac{5π}{6}$时,四边形OACB的面积取得最大值.
点评 本题主要余弦定理的应用,两角和差的正弦公式、正弦函数的最值,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com