
分析 利用函数的奇偶性判断①,根据y=sinx与y=x的图象关系判断②,令f(x)=0求出零点,结合定义域即可判断③,利用函数图象判断④.
解答 解:对于①,f(x)的定义域为{x|x≠0},关于原点对称,
∵f(-x)=$\frac{sin(-x)}{-x}$=$\frac{sinx}{x}=f(x)$,∴f(x)是偶函数,
∴f(x)的图象关于y轴对称,故①正确;
对于②,∵(sinx)′|x=0=cos0=1,
∴y=sinx在(0,0)处的切线为y=x,
∴|sinx|<|x|(x≠0),
∴|f(x)|=$|\frac{sinx}{x}|$<1,故②正确;
对于③,令f(x)=0得sinx=0,∴x=kπ,k∈{k∈Z|k≠0},
∴f(x)的图象与x轴的交点中,距离原点最近的两个交点距离为2π,其余相邻的交点距离为π,
故③错误;
对于④,联立方程组$\left\{\begin{array}{l}{y=\frac{sinx}{x}}\\{y=kx}\end{array}\right.$得kx2=sinx(k≠0,x≠0),
根据y=kx2与y=sinx的函数图象可知两图象必有1交点,
∴函数y=f(x)的图象与直线y=kx有且仅有一个公共点,故④正确.
故答案为:①②④.
点评 本题考查了函数及其图象的性质,函数零点的判断,属于中档题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {2} | C. | {2,5} | D. | {5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
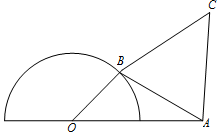 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
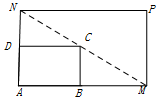 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com