
分析 设A(x1,y1),B(x2,y2),代入椭圆方程,设$\overrightarrow{AM}$=t$\overrightarrow{MB}$,$\overrightarrow{AP}$=-t$\overrightarrow{PB}$,M(x,y),运用向量的共线的坐标表示,计算
x0x,y0y,即可得证.
解答 证明:设A(x1,y1),B(x2,y2),
可得$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
设$\overrightarrow{AM}$=t$\overrightarrow{MB}$,$\overrightarrow{AP}$=-t$\overrightarrow{PB}$,M(x,y),
可得$\left\{\begin{array}{l}{x=\frac{{x}_{1}+t{x}_{2}}{1+t}}\\{y=\frac{{y}_{1}+t{y}_{2}}{1+t}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{0}=\frac{{x}_{1}-t{x}_{2}}{1-t}}\\{{y}_{0}=\frac{{y}_{1}-t{y}_{2}}{1-t}}\end{array}\right.$,
即有x0x=$\frac{{{x}_{1}}^{2}-{t}^{2}{{x}_{2}}^{2}}{1-{t}^{2}}$,y0y=$\frac{{{y}_{1}}^{2}-{t}^{2}{{y}_{2}}^{2}}{1-{t}^{2}}$,
则$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=$\frac{1}{1-{t}^{2}}$[($\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$)-t2($\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$)]
=$\frac{1}{1-{t}^{2}}$•(1-t2)=1.
点评 本题考查椭圆的方程和运用,考查向量的共线的坐标表示,以及化简整理的能力,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
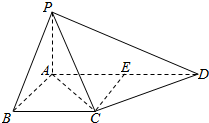 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
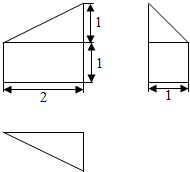
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com