练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数是定义在 上的偶函数，当时， ）.

    （1）当时，求的解析式；

    （2）若，试判断的上单调性，并证明你的结论；

    （3）是否存在，使得当时， 有最大值.

    【答案】（1）；（2）详见解析；（3）.

    【解析】试题分析：(1)根据分段函数的奇偶性可得当时，求的解析式；（2）由于可得恒成立，得在上为增函数，根据对称性得在上为减函数；（3）讨论时，当时两种情况，研究单调性并求最值，舍去不合题意的情况，即可得结论.

    试题解析： (1)设，则，又是偶函数， .

    （2）,又，即在上为增函数.

    （3）当时， 在上是增函数， ，（不合题意，舍去）.

    当时， ，令，如下表：

    ↗

    最大值

    ↘

    在处取得最大值，满足条件，当时，

    在上单调递减， 在无最大值，所以存在，使在上有最大值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在某地区某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居众显示可以过正常生活，有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”，根据连续7天的新增病例数计算，下列各选项中，一定符合上述指标的是( )

    ①平均数≤3；②标准差S≤2；③平均数≤3且标准差S≤2；④平均数≤3且极差小于或等于2；⑤众数等于1且极差小于或等于1.

    A．①② B．③④

    C．③④⑤ D．④⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业拟生产一种如图所示的圆柱形易拉罐（上下底面及侧面的厚度不计）.易拉罐的体积为 ，设圆柱的高度为 ，底面半径为 ，且.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为元/ ，易拉罐上下底面的制造费用均为元/ （， 为常数，且）.

    （1）写出易拉罐的制造费用（元）关于的函数表达式，并求其定义域；

    （2）求易拉罐制造费用最低时的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3+ax2+bx+a2.

    （I）若f（x）在x=1处有极值10，求a，b的值；

    （II）若当a=-1时，f（x）<0在x∈[1，2]恒成立，求b的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设关于x的函数y＝2cos2x－2acosx－(2a＋1)的最小值为f(a)，试确定满足f(a)＝的a的值，并求此时函数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a是实数，函数f(x)＝ (x－a)．

    (1)求函数f(x)的单调区间；

    (2)设g(a)为f(x)在区间[0,2]上的最小值．

    ①写出g(a)的表达式；

    ②求a的取值范围，使得－6≤g(a)≤－2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x3＋x2＋x(0<a<1，x∈R)．若对于任意的三个实数x1，x2，x3∈[1,2]，都有f(x1)＋f(x2)>f(x3)恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】不等式－kx＋1≤0的解集非空，则k的取值范围为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费支出与销售额（单位：万元）之间有如下对应数据：

    （1）求回归直线方程；

    （2）试预测广告费支出为万元时，销售额多大？

    （3）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过的概率.(参考数据： .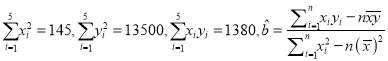

    查看答案和解析>>

    同步练习册答案