
分析 (1)利用三种方程的互化方法将直线l与圆C的极坐标方程化为直角坐标方程
(2)求出圆心到直线的距离,即可求直线l与圆C相交所得的弦长.
解答 解:(1)直线l的方程是$ρsin(θ+\frac{π}{4})=\sqrt{2}$,即ρcosθ+ρsinθ=2,直角坐标方程x+y-2=0;
圆C的方程是ρ=4,直角坐标方程是x2+y2=16,半径等于4.
(2)圆心到直线的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,弦长为2$\sqrt{16-2}$=2$\sqrt{14}$.
点评 本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式,直线和圆的位置关系,属于基础题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为2的正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为2的正方形,PD=DC,E,F分别是AB,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)≥f(b)且当x>0时f(b-x)≥f(b+x) | B. | f(x)≥f(b)且当x>0时f(b-x)≤f(b+x) | ||
| C. | f(x)≥f(a)且当x>0时f(a-x)≥f(a+x) | D. | f(x)≥f(a)且当x>0时f(a-x)≤f(a+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
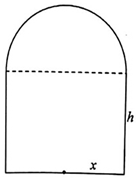 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
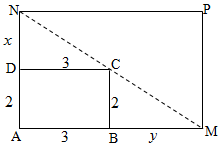 如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.
如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com