
已知函数 ∈R).
∈R).
(1)若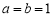 ,求
,求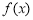 点(
点(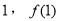 )处的切线方程;
)处的切线方程;
(2)设a≤0,求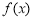 的单调区间;
的单调区间;
(3)设a<0,且对任意的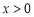 ,
,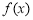 ≤
≤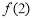 ,试比较
,试比较 与
与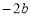 的大小.
的大小.
(1)2x-2y-3=0;(2)递增区间(0,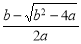 ),递减区间(
),递减区间(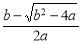 ,+∞);(3)ln(-a)<-2b.
,+∞);(3)ln(-a)<-2b.
【解析】
试题分析:(1)a=b=1时,直接求导数,可得f '(1)和f(1)的值,利用点斜式可写出切线方程;(2)a<0时,根据b的范围和导函数值的符号,可求出相应单调区间;(3)由题意知函数f(x)在x=2处取得最大值,得到a与b的等量关系式,然后比差,再利用函数的思想,得出ln(-a)与-2b的大小.
试题解析:(1)a=b=1时, ,
,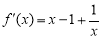 ,
,
∴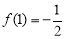 ,
,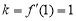 , 2分
, 2分
故f(x)点(1,f(1))处的切线方程是2x-2y-3=0. 3分
(2)由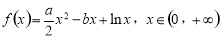 ,得
,得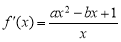 .
.
(1)当a=0时,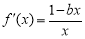 .
.
①若b≤0,
由x>0知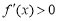 恒成立,即函数f(x)的单调递增区间是(0,+∞).
恒成立,即函数f(x)的单调递增区间是(0,+∞).
5分
②若b>0,
当 时,
时,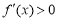 ;当
;当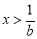 时,
时,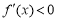 .
.
即函数f(x)的单调递增区间是(0,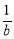 ),单调递减区间是(
),单调递减区间是(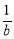 ,+∞).
,+∞).
7分
(2)当a<0时, ,得
,得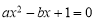 ,
,
由△=b2-4a>0得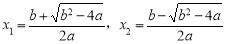 .
.
显然, ,
,
当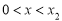 时,
时,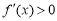 ,函数f(x)的单调递增,
,函数f(x)的单调递增,
当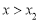 时,
时,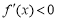 ,函数
,函数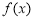 的单调递减,
的单调递减,
所以函数f(x)的单调递增区间是(0,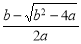 ),
),
单调递减区间是(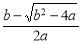 ,+∞). 9分
,+∞). 9分
综上所述:
当a=0,b≤0时,函数f(x)的单调递增区间是(0,+∞);
当a=0,b>0时,函数f(x)的单调递增区间是(0,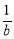 ),单调递减区间是(
),单调递减区间是(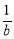 ,+∞);
,+∞);
当a<0时,函数f(x)的单调递增区间是(0,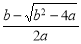 ),
),
单调递减区间是(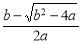 ,+∞). 10分
,+∞). 10分
(3)由题意知函数f(x)在x=2处取得最大值.
由(2)知,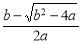 是f(x)的唯一的极大值点,
是f(x)的唯一的极大值点,
故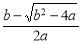 =2,整理得-2b=-1-4a.
=2,整理得-2b=-1-4a.
于是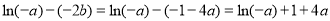
令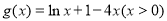 ,则
,则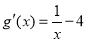 .
.
令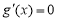 ,得
,得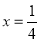 ,当
,当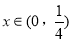 时,
时,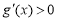 ,g(x)单调递增;
,g(x)单调递增;
当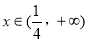 时,
时,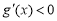 ,g(x)单调递减.
,g(x)单调递减.
因此对任意x>0,g(x)≤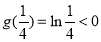 ,又-a>0,
,又-a>0,
故g(-a)<0,即ln(-a)+1+4a<0,即ln(-a)<-1-4a=-2b,
∴ ln(-a)<-2b. 14分
考点:利用导数研究函数性质,不等式


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 6 |
| 3 |
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试文科数学试卷(解析版) 题型:选择题
设p:(x-2)(y-5)≠0;q:x≠2或y≠5,则p是q的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试理科数学试卷(解析版) 题型:填空题
已知向量a=(1,2),b=(2,0),若向量λa+b与向量c=(1,-2)共线,则实数λ=______.
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:解答题
已知向量m=(sinωx,cosωx),n=(cosωx,cosωx),其中ω>0,函数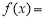 2m·n-1的最小正周期为π.
2m·n-1的最小正周期为π.
(1)求ω的值;
(2)求函数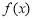 在[
在[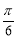 ,
,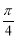 ]上的最大值.
]上的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:选择题
记函数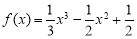 在
在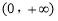 的值域为M,g(x)=(x+1)2+a在
的值域为M,g(x)=(x+1)2+a在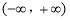 的值域为N,若
的值域为N,若 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
(A)a≥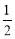 (B)a≤
(B)a≤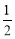
(C)a≥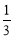 (D) a≤
(D) a≤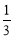
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试理科数学试卷(解析版) 题型:填空题
已知数列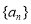 为等差数列,
为等差数列,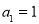 ,公差
,公差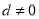 ,
,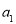 、
、 、
、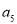 成等比数列,则
成等比数列,则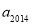 的值为____________.
的值为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com