
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在与
在与![]() 轴的交点
轴的交点![]() 处的切线斜率为-1.
处的切线斜率为-1.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:当![]() 时,
时, 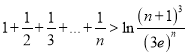 .
.
【答案】(1)![]() ,
, ![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)证明见解析;(3)证明见解析.
上单调递增;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)求出函数的f′(x)=ex﹣a.通过f′(x)=ex﹣2>0,即可求解函数f(x)在区间(﹣∞,ln2)上单调递减,在(ln2,+∞)上单调递增.
(2)求出f(x)的最小值,化简f(x)≥1﹣ln4.构造g(x)=ex﹣x2﹣1,通过g′(x)>0.判断g(x)在(0,+∞)上单调递增,得到g(x)>g(0),推出结果.
(3)首先证明:当x>0时,恒有![]() .令
.令![]() ,则h′(x)=ex﹣x2.推出h(x)在(0,+∞)上单调递增,得到x+ln3>3lnx.利用累加法推出
,则h′(x)=ex﹣x2.推出h(x)在(0,+∞)上单调递增,得到x+ln3>3lnx.利用累加法推出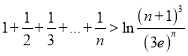 .
.
试题解析:
(1)由![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .所以
.所以![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)证明:由(1)知![]() .
.
所以![]() ,即
,即![]() ,
, ![]() .
.
令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
(3)首先证明:当![]() 时,恒有
时,恒有![]() .
.
证明如下:令![]() ,则
,则![]() .
.
由(2)知,当![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() .所以
.所以![]() ,即
,即![]() .依次取
.依次取![]() ,代入上式,则
,代入上式,则![]() ,
, ![]() ,
, ![]()
![]() .
.
以上各式相加,有![]() .
.
所以![]() ,
,
所以, ![]()
即![]() .
.


科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
①我离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室里取了作业本再回家;
②我放学回家骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;

③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
A.(1)(2)(4)B.(4)(1)(2)C.(4)(1)(3)D.(4)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽配厂生产某种零件,每个零件的出厂单价为60元,为了鼓励更多销售商订购,该厂决定当一次订购超过100个时,每多订购一个,订购的全部零件的出厂单价就降低![]() 元,但实际出厂单价不低于51元.
元,但实际出厂单价不低于51元.
![]() 当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
![]() 设一次订购量为x个,零件的实际出厂单价为p元,写出函数
设一次订购量为x个,零件的实际出厂单价为p元,写出函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,一个顶点
轴上,一个顶点![]() ,且右焦点到直线
,且右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆的方程.
(2)若点![]() 为椭圆的下顶点,是否存在斜率为
为椭圆的下顶点,是否存在斜率为![]() ,且过定点
,且过定点![]() 的直线
的直线![]() ,使
,使![]() 与椭圆交于不同两点
与椭圆交于不同两点![]() ,
,![]() 且满足
且满足![]() ? 若存在,求直线
? 若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”.区间
为“可等域函数”.区间![]() 为函数的一个“可等域区间”.给出下列三个函数:
为函数的一个“可等域区间”.给出下列三个函数:
①![]() ;②
;②![]() ;③
;③![]() ;
;
则其中存在唯一“可等域区间”的“可等域函数”的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图.
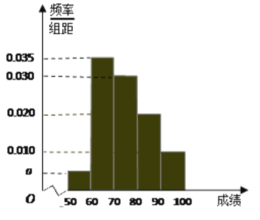
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com