
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图.
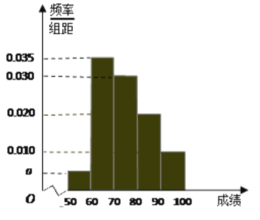
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
【答案】(1)![]() (2)74.5(3)
(2)74.5(3)![]()
【解析】
(1)根据概率和为1,即所有矩形的面积和为1,建立等式关系,即可求;(2)均值为各组组中值与该组频率之积的和;(3)先分别求出3,4,5组的人数,再利用古典概型知识求解.
(1)由题意得![]() ,所以
,所以![]() .
.
(2)由直方图分数在![]() 的频率为0.05,
的频率为0.05,![]() 的频率为0.35,
的频率为0.35,![]() 的频率为0.30,
的频率为0.30,![]() 的频率为0.20,
的频率为0.20,![]() 的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:
的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:![]() .
.
(3)由直方图,得:第3组人数为![]() .第4组人数为
.第4组人数为![]() 人,第5组人数为
人,第5组人数为![]() 人.所以利用分层抽样在60名学生中抽取6名学生,第3、4、5组分别抽取3人、2人、1人.设第3组的3位同学为
人.所以利用分层抽样在60名学生中抽取6名学生,第3、4、5组分别抽取3人、2人、1人.设第3组的3位同学为![]() ,
,![]() ,
,![]() ,第4组的2位同学为
,第4组的2位同学为![]() ,
,![]() ,第5组的1位同学为
,第5组的1位同学为![]() ,则从六位同学中抽两位同学有15种可能如下:
,则从六位同学中抽两位同学有15种可能如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其中恰有1人的分数不低于 90(分)的情形有:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,共5种.所以其中第4组的2位同学至少有一位同学入选的概率为
,共5种.所以其中第4组的2位同学至少有一位同学入选的概率为![]() .
.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在与
在与![]() 轴的交点
轴的交点![]() 处的切线斜率为-1.
处的切线斜率为-1.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:当![]() 时,
时, 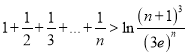 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【安徽省滁州市2018届高三上学期期末考试数学】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
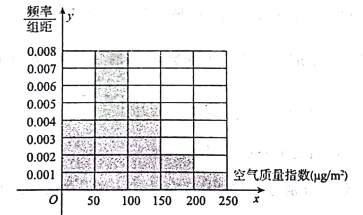
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,记这
天进行空气颗粒物分析,记这![]() 天中空气质量指数在
天中空气质量指数在![]() 的天数为
的天数为![]() ,求
,求![]() 的分布列;
的分布列;
(3)以频率估计概率,根据上述情况,若在一年![]() 天中随机抽取
天中随机抽取![]() 天,记空气质量指数在
天,记空气质量指数在![]() 以上(含
以上(含![]() )的天数为
)的天数为![]() ,求
,求![]() 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com