练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．已知抛物线Г：x2=2y，过点A（0，-2）和B（t，0）的直线与抛物线没有公共点，则实数t的取值范围是（-∞，-1）∪（1，+∞）．

    分析 设过A的直线方程，与抛物线方程联立，根据判别式求得k，求得过A的抛物线的切线与y=0的交点，则当过点A（0，-2）和B（t，0）的直线与抛物线C没有公共点，进而求得t的范围．

    解答 解：设过A的直线方程为y=kx-2，与抛物线方程联立得x2-2kx+4=0，
    △=4k2-16=0，k=±2，求得过A的抛物线的切线与y=0的交点为（±1，0），
    则当过点A（0，-2）和B（t，0）的直线与抛物线C没有公共点，
    实数t的取值范围是（-∞，-1）∪（1，+∞），
    故答案为：（-∞，-1）∪（1，+∞）．

    点评 本题主要考查了直线与圆锥曲线的综合问题．直线与圆锥曲线有无公共点或有几个公共点的问题，实际上是研究它们的方程组成的方程是否有实数解成实数解的个数问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知二次函数f（x）=x2+ax+b2，若a，b在区间[0，2]内等可能取值，求f（x）=0有实数解的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知点M的直角坐标为（-1，-$\sqrt{3}$，3），则它的柱坐标是（　　）
    A．（2，$\frac{π}{3}$，3）B．（2，$\frac{2π}{3}$，3）C．（2，$\frac{4π}{3}$，3）D．（2，$\frac{5π}{3}$，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若z=（a2-1）+（a-1）i为纯虚数，其中a∈R，则$\frac{{{a^2}+i}}{1+ai}$等于（　　）
    A．-iB．iC．1D．1或i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

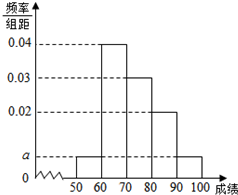    7．某校100名学生数学竞赛成绩的频率分布直方图如图所示，成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]，则该次数学成绩在[50，60）内的人数为（　　）
    A．20B．15C．10D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知 f（x）=$\frac{x}{2x+1}$（x＞0），f1（x）=f（x），fn+1（x）=f（fn（x）），n∈N*，则 fs（x）在[$\frac{1}{2}$，1]上的最小值是$\frac{1}{12}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

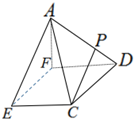    4．如图，在四棱锥A-CDEF中，四边形CDFE为直角梯形，CE∥DF，EF⊥FD，AF⊥平面CEFD，P为AD中点，EC=$\frac{1}{2}$FD．
    （Ⅰ）求证：CP∥平面AEF；
    （Ⅱ）设EF=2，AF=3，FD=4，求点F到平面ACD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=lnx+$\frac{1}{x}$-1．
    （1）求函数的单调性；
    （2）证明：ln（n+1）!＞2n-4$\sqrt{n+1}$（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．对于任意两个复数z1=x1+y1i，z2=x2+y2i（其中x1，y1，x2，y2∈R），定义运算⊙为：z1⊙z2=x1x2+y1y2，设非零复数ω1，ω2满足ω1⊙ω2=0，ω1，ω2在平面直角坐标系中对应的点分别为W1，W2，那么在△W1OW2（其中O为坐标原点）中，∠W1OW2的大小为$\frac{π}{2}$．

    查看答案和解析>>

    同步练习册答案