
分析 易知f(x)=$\frac{x}{2x+1}$在[$\frac{1}{2}$,1]上是增函数,且f(x)>0;从而依次代入化简即可.
解答 解:f(x)=$\frac{x}{2x+1}$在[$\frac{1}{2}$,1]上是增函数,且f(x)>0;
f1(x)=f(x)=$\frac{x}{2x+1}$,在[$\frac{1}{2}$,1]上递增,
故f1(x)min=$\frac{1}{4}$,
f2(x)min=f(f1(x)min)=f($\frac{1}{4}$)=$\frac{1}{6}$,
f3(x)min=f(f2(x)min)=f($\frac{1}{6}$)=$\frac{1}{8}$,
f4(x)min=f(f3(x)min)=f($\frac{1}{8}$)=$\frac{1}{10}$,
f5(x)min=f(f4(x)min)=f($\frac{1}{10}$)=$\frac{1}{12}$.
故答案为:$\frac{1}{12}$.
点评 本题考查了函数的性质的判断与应用,主要是单调性的运用,同时考查整体思想的应用,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
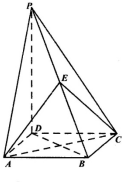 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
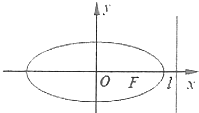 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点到直线$l:x=\frac{a^2}{c}$的距离为$\frac{4\sqrt{5}}{5}$,离心率$e=\frac{{\sqrt{5}}}{3}$,A,B是椭圆上的两动点,动点P满足$\overrightarrow{OP}=\overrightarrow{OA}+λ\overrightarrow{OB}$,(其中λ为常数).
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点到直线$l:x=\frac{a^2}{c}$的距离为$\frac{4\sqrt{5}}{5}$,离心率$e=\frac{{\sqrt{5}}}{3}$,A,B是椭圆上的两动点,动点P满足$\overrightarrow{OP}=\overrightarrow{OA}+λ\overrightarrow{OB}$,(其中λ为常数).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2i | B. | 1-i | C. | 2i | D. | 1+i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com