
| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
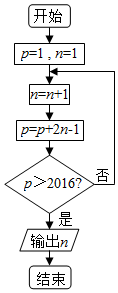
分析 框图首先给循环变量n赋值1,给累加变量p赋值1,然后执行运算n=n+1,p=p+2n-1,然后判断p>2016是否成立,不成立循环执行n=n+1,p=p+2n-1,成立时算法结束,输出n的值.且由框图可知,程序执行的是求等差数列的前n项和问题.当前n项和大于2016时,输出n的值.
解答 解:框图首先给循环变量n赋值1,给累加变量p赋值1,
执行n=1+1=2,p=1+(2×2-1)=1+3=4;
判断4>2016不成立,
执行n=2+1=3,p=1+3+(2×3-1)=1+3+5=9;
判断9>2016不成立,
执行n=3+1=4,p=1+3+5+(2×4-1)=1+3+5+7=16;
…
由上可知,程序运行的是求首项为1,公差为2的等差数列的前n项和,
由p=$\frac{(1+2n-1)n}{2}$>2016,且n∈N*,得n=45.
故选:C.
点评 本题考查了程序框图,考查了等差数列的前n项和公式,解答此题的关键是能够由框图看出程序执行的是求等差数列前n项和的运算,此题是基础题.


科目:高中数学 来源: 题型:解答题
 某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
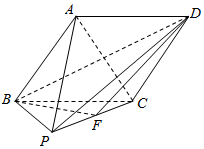 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
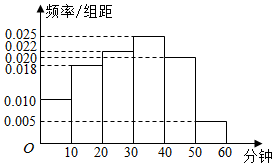 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 9个 | C. | 12个 | D. | 24个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com