
设函数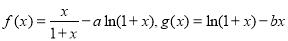 .
.
(1)若函数 在
在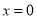 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)是否存在实数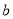 ,使得关于
,使得关于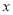 的不等式
的不等式 在
在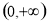 上恒成立?若存在,求出
上恒成立?若存在,求出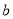 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)记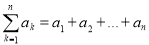 ,证明:不等式
,证明:不等式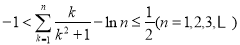 .
.
(1)0,(2)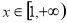 (3)证明见解析
(3)证明见解析
【解析】
试题分析:(1)解决类似的问题时,注意区分函数的最值和极值.求函数的最值时,要先求函数 在区间
在区间 内使
内使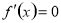 的点,再计算函数
的点,再计算函数 在区间内所有使
在区间内所有使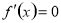 的点和区间端点处的函数值,最后比较即得.(2)有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.(3)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
的点和区间端点处的函数值,最后比较即得.(2)有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.(3)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
试题解析:(1)由已知得:
 ,
,
且函数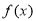 在
在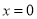 处有极值
处有极值
∴ ,
,
即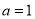
∴
∴
当 时,
时, ,
,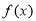 单调递增;
单调递增;
当 时,
时,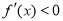 ,
,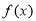 单调递减;
单调递减;
∴函数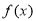 的最大值为
的最大值为
(2)由已知得:
1.若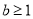 ,则
,则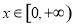 时,
时,
∴ 在
在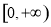 上为减函数,
上为减函数,
∴ 在
在 上恒成立;
上恒成立;
2.若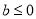 ,则
,则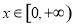 时,
时,
∴ 在
在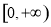 上为增函数,
上为增函数,
∴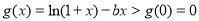 ,不能使
,不能使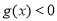 在
在 上恒成立;
上恒成立;
3.若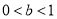 ,则
,则 时,
时, ,
,
当 时,
时, ,∴
,∴ 在
在 上为增函数,
上为增函数,
此时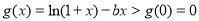 ,
,
∴不能使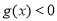 在
在 上恒成立;
上恒成立;
综上所述, 的取值范围是
的取值范围是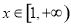
(3) 由(1)、(2)得: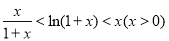
取 得:
得:
令 ,
,
则 ,
, .
.
因此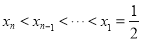 .
.
又 ,
,
故
因此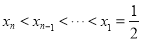 .
.
又 ,
,
故

考点:(1)导数与最值(2)求参数取值范围(3)证明不等式.


科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三理科数学试卷(解析版) 题型:选择题
形如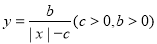 的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数
的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数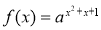
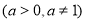 有最小值,则当
有最小值,则当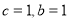 时的“囧函数”与函数
时的“囧函数”与函数 的图像交点个数为________个.( )
的图像交点个数为________个.( )
A. B.
B.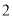 C.
C.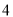 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三12月月考文科数学试卷(解析版) 题型:选择题
若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0外切,则m=( )
A.21 B.19 C.9 D.-11
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三12月月考理科数学试卷(解析版) 题型:解答题
本小题满分12分)已知函数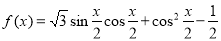 ,
,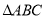 三个内角
三个内角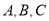 的对边分别为
的对边分别为 .
.
(Ⅰ)求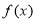 的单调递增区间及对称轴的方程;
的单调递增区间及对称轴的方程;
(Ⅱ)若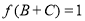 ,
,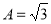
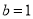 ,求角
,求角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三12月月考理科数学试卷(解析版) 题型:选择题
已知P是以F1,F2为焦点的椭圆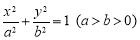 上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα= ,sin(α+β)=
,sin(α+β)=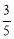 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A.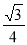 B.
B. C.
C.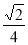 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com