
 物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型,如果物体的初始温度为θ1℃,空气温度为θ0℃,则tmin后物体的温度f(t)满足:f(t)=θ0+(θ1-θ0)•e-kt(其中k为正的常数,e=2.71828…为自然对数的底数),现有65℃的物体,放在15℃的空气中冷却,5min以后物体的温度是45℃.
物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型,如果物体的初始温度为θ1℃,空气温度为θ0℃,则tmin后物体的温度f(t)满足:f(t)=θ0+(θ1-θ0)•e-kt(其中k为正的常数,e=2.71828…为自然对数的底数),现有65℃的物体,放在15℃的空气中冷却,5min以后物体的温度是45℃.分析 (Ⅰ)通过将θ1=65,θ0=15,当t=5时,θ=45代入公式计算可知k的值;
(Ⅱ)根据(Ⅰ)的函数的表达式进行求解即可.
(Ⅲ)根据指数函数的图象和性质进行作图即可.
解答 解:(Ⅰ)由题意可知,θ1=65,θ0=15,当t=5时,θ=45,
于是e-5k=$\frac{3}{5}$
化简得:-5k=ln$\frac{3}{5}$,即k=$\frac{1}{5}$ln$\frac{5}{3}$;
(Ⅱ)由(I)可知f(t)=15+50e-kt,(其中k=$\frac{1}{5}$ln$\frac{5}{3}$),
∴由25.8=15+50e-kt,得e-kt=$\frac{27}{125}$,
结合k=$\frac{1}{5}$ln$\frac{5}{3}$,得($\frac{3}{5}$)e${\;}^{\frac{t}{5}}$t=$\frac{27}{125}$,得t=15.
∴从开始冷却,经过15min物体的温度是25.8°.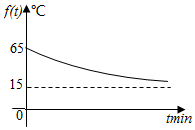
(Ⅲ)由f(t)=15+50e-kt,(其中k=$\frac{1}{5}$ln$\frac{5}{3}$),
知函数的图象如图:
图象在第一象限内,过点(0,65),在[0,+∞)上是减函数,y=15是渐近线.
点评 本题考查函数模型的选择与应用,考查运算求解能力,注意解题方法的积累,考查学生的计算能力.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
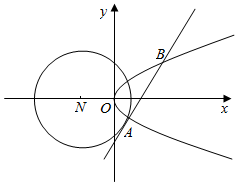 如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
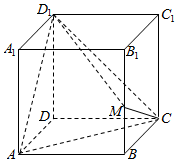
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.
在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com