练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．下列说法中：
    ①在空间直角坐标系中，在x轴上的点的坐标一定可记为（0，b，c）；
    ②在空间直角坐标系中，在yOz平面上的点的坐标一定可记为（0，b，c）；
    ③在空间直角坐标系中，在z轴上的点的坐标一定可记为（0，0，c）；
    ④在空间直角坐标系中，在xOz平面上的点的坐标一定可记为（a，0，c）．
    其中正确的个数是（　　）
    A．1B．2C．3D．4

    分析 根据空间向量的特点即可判断．

    解答 解：①在空间直角坐标系中，在x轴上的点的坐标一定可记为（a，0，0），故①错误，
    ②在空间直角坐标系中，在yOz平面上的点的坐标一定可记为（0，b，c），故②正确，
    ③在空间直角坐标系中，在z轴上的点的坐标一定可记为（0，0，c）；故③正确，
    ④在空间直角坐标系中，在xOz平面上的点的坐标一定可记为（a，0，c），故④正确，
    故正确的个数为3个，
    故选：C．

    点评 本题考查了空间向量的坐标问题，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．广丰一中现有教职工180人，其中高级职称30人，中级职称90人，一般职员60人，现抽取30人进行分层抽样，则各职称人数分别为（　　）
    A．5，15，10B．3，18，9C．7，13，10D．5，12，9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．计算下列各题：
    （1）${（0.027）^{-\frac{1}{3}}}-{（-\frac{1}{7}）^{-2}}+{（2\frac{7}{9}）^{\frac{1}{2}}}-{（\sqrt{2}-1）^0}$
    （2）${log_5}35+2{log_{\frac{1}{2}}}\sqrt{2}-{log_5}\frac{1}{50}-{log_5}14+{5^{{{log}_5}3}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型，如果物体的初始温度为θ1℃，空气温度为θ0℃，则tmin后物体的温度f（t）满足：f（t）=θ0+（θ1-θ0）•e-kt（其中k为正的常数，e=2.71828…为自然对数的底数），现有65℃的物体，放在15℃的空气中冷却，5min以后物体的温度是45℃．
    （Ⅰ）求k的值；
    （Ⅱ）求从开始冷却，经过多少时间物体的温度是25.8℃？
    （Ⅲ）运用上面的数据，作出函数f（t）的图象的草图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

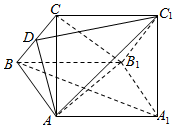    8．如图，三棱柱ABC-A1B1C1的侧面AA1B1B为正方形，侧面BB1C1C菱形，∠CBB1=60°，AB⊥平面BB1C1C，且D是BC的中点．
    （1）求证：A1B∥平面ADC1；
    （2）若AB=2，求三棱锥B1-ABC体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知P：方程X2+mX+m+3=0有一正一负两根，q：不等式mX2+2X+1＞0恒成立，如果p或q为真，p且q为假，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．直三棱柱ABC-A1B1C1中，AB=AC=2，$∠BAC=\frac{2π}{3}$，AA1=4，则该三棱柱的外接球的体积为$\frac{{64\sqrt{2}π}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

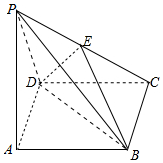    2．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD是正三角形，PD⊥CD，E为PC的中点．
    （Ⅰ）求证：平面ABE⊥平面PCD；
    （Ⅱ）求二面角B-DE-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=$\left\{\begin{array}{l}{|lnx|，x＞0}\\{{x}^{2}+4x+1，x≤0}\end{array}\right.$，g（x）=f（x）-a
    （1）当a=2时，求函数g（x）的零点；
    （2）若函数g（x）有四个零点，求a的取值范围；
    （3）在（2）的条件下，记g（x）得四个零点分别为x1，x2，x3，x4，求x1+x2+x3+x4的取值范围．

    查看答案和解析>>

    同步练习册答案