
分析 P:方程X2+mX+m+3=0有一正一负两根,可得$\left\{\begin{array}{l}{△={m}^{2}-4(m+3)>0}\\{m+3<0}\end{array}\right.$,解得m范围.q:不等式mX2+2X+1>0恒成立,m=0时不满足题意,舍去;当m≠0时,$\left\{\begin{array}{l}{m>0}\\{△=4-4m<0}\end{array}\right.$,解得m范围.如果p或q为真,p且q为假,可得p与q必然一真一假即可得出.
解答 解:P:方程X2+mX+m+3=0有一正一负两根,∴$\left\{\begin{array}{l}{△={m}^{2}-4(m+3)>0}\\{m+3<0}\end{array}\right.$,解得m<-3.
q:不等式mX2+2X+1>0恒成立,m=0时不满足题意,舍去;当m≠0时,$\left\{\begin{array}{l}{m>0}\\{△=4-4m<0}\end{array}\right.$,解得m>1.
如果p或q为真,p且q为假,
∴p与q必然一真一假,∴$\left\{\begin{array}{l}{m<-3}\\{m≤1}\end{array}\right.$或$\left\{\begin{array}{l}{m≥-3}\\{m>1}\end{array}\right.$,
解得m<-3或m>1.
∴m的取值范围是m<-3或m>1.
点评 本题考查了一元二次方程有实数根与判别式的关系、一元二次不等式的解集与判别式的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
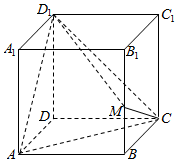
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点
如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.
在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
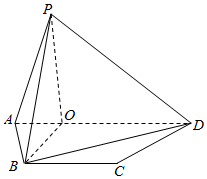 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{121}{25}$ | B. | $\frac{81}{16}$ | C. | $\frac{16}{9}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com