
分析 (1)设出切点P(x1,ex1),求出y=f(x)的导数,可得切线的斜率和方程,代入原点求得切点坐标,可得切线的斜率;
(2)设l2与曲线y=g(x)的切点为Q(x2,y2),可得切线的斜率和方程,由k1=e,可得lnx2-1+$\frac{1}{{x}_{2}}$-$\frac{1}{e}$=0,令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$,求出导数和单调区间,讨论x2∈(0,1),x2∈(1,+∞),由零点存在定理,即可得到所求范围.
解答 解:(1)对f(x)求导,得f′(x)=ex,
设经过坐标原点作曲线y=f(x)的切线l1,其切点为P(x1,ex1),
即有切线的斜率为k1=ex1,切线的方程为y-ex1=ex1(x-x1),
代入原点(0,0),可得-ex1=ex1(-x1),可得x1=1,
即有k1=e;
(2)证明:由(1)可得k1=e.
由题意知,切线l2的斜率为k2=$\frac{1}{{k}_{1}}$=$\frac{1}{e}$,
l2的方程为y=k2x=$\frac{1}{e}$x.
设l2与曲线y=g(x)的切点为Q(x2,y2),
则k2=f′(x2)=$\frac{1}{{x}_{2}}$-a=$\frac{1}{e}$=$\frac{{y}_{2}}{{x}_{2}}$,
所以y2=$\frac{{x}_{2}}{e}$=1-ax2,a=$\frac{1}{{x}_{2}}$-$\frac{1}{e}$.
又因为y2=lnx2-a(x2-1),消去y2和a后,
整理得lnx2-1+$\frac{1}{{x}_{2}}$-$\frac{1}{e}$=0.
令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$,
则m′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x2∈(0,1),因为m($\frac{1}{e}$)=-2+e-$\frac{1}{e}$>0,m(1)=-$\frac{1}{e}$<0,
所以x2∈($\frac{1}{e}$,1),
而a=$\frac{1}{{x}_{2}}$-$\frac{1}{e}$在x2∈($\frac{1}{e}$,1)上单调递减,
所以1-$\frac{1}{e}$<a<e-$\frac{1}{e}$.
若x2∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x2=e,
所以a=$\frac{1}{{x}_{2}}$-$\frac{1}{e}$=0与a>0矛盾.
综上可知,1-$\frac{1}{e}$<a<e-$\frac{1}{e}$.
点评 本题考查利用导数求曲线的切线问题和判断函数的单调性及研究不等式恒成立问题,注意运用分类讨论和构造函数法,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,1) | C. | (0,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
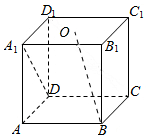
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com