解:(1)由已知设l
AB:y=kx+

①
又设抛物线C:x
2=ay(a>0)②
由①②得x
2-akx-

=0
设A(x
A,y
A),B(x
B,y
B),,则x
A•x
B=-

由弦长公式得
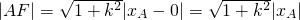
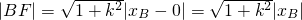
∴|AF|•|BF|=(1+k
2)×|

|
而|AF|•|BF|=1+k
2,所以a=2,即抛物线方程为C:x
2=2y
(2)设M(x
M,y
M),N(x
N,y
N),由
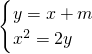
?x
2-2x-2m=0
而△4+8m>0(m>0)
则x
M+x
N=2,x
M•x
N=-2m,

,
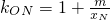
不妨设x
M<x
N,由于m>0,则x
M<0<x
N令
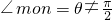
,则ON到OM的角为θ,且满足
tanθ=

令
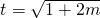
,则
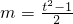
,t>1且t≠

∴tanθ=
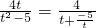
函数y=x与

在(0,+∞)上皆为增函数
∴t-

∈(-4,0)∪(0,+∞)
∴
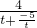
∈(-∞,-1)∪(0,+∞)
则θ∈(0,

)∪(

,

),又m=2时,∠MON=θ=

∴∠MON∈(0,

)
分析:(1)设出直线AB和抛物线C的方程并联立消y,在利用弦长公式求出AF和BF代入|AF|•|BF|=1+k
2.即可求出抛物线C的方程;
(2)先把直线l的方程与抛物线C的方程联立消y,求出M、N两点横坐标之间的关系,再求出直线ON和MO的斜率,利用到角公式求出∠MON的正切.最后在利用函数的思想求出∠MON的正切值的范围,进而求出∠MON的取值范围.
点评:本题综合考查了直线与抛物线的位置关系以及弦长公式的应用问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.

 ),直线AB的斜率为k,且满足|AF|•|BF|=1+k2.
),直线AB的斜率为k,且满足|AF|•|BF|=1+k2. ①
① =0
=0
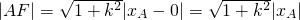
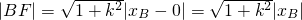
 |
|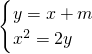 ?x2-2x-2m=0
?x2-2x-2m=0 ,
,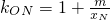
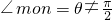 ,则ON到OM的角为θ,且满足
,则ON到OM的角为θ,且满足
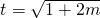 ,则
,则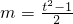 ,t>1且t≠
,t>1且t≠
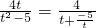
 在(0,+∞)上皆为增函数
在(0,+∞)上皆为增函数 ∈(-4,0)∪(0,+∞)
∈(-4,0)∪(0,+∞)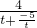 ∈(-∞,-1)∪(0,+∞)
∈(-∞,-1)∪(0,+∞) )∪(
)∪( ,
, ),又m=2时,∠MON=θ=
),又m=2时,∠MON=θ=
 )
)

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.