
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)求出![]() 的导数,通过讨论
的导数,通过讨论![]() 的取值范围,确定函数的单调区间,从而求出函数的最大值和最小值;(2)求出
的取值范围,确定函数的单调区间,从而求出函数的最大值和最小值;(2)求出![]() 的导数,通过讨论
的导数,通过讨论![]() 的取值范围,确定函数的单调区间,从而求出
的取值范围,确定函数的单调区间,从而求出![]() 的取值范围.
的取值范围.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() ;
;
当![]() ,有
,有![]() ;当
;当![]() ,有
,有![]() ,
,
∴![]() 在区间
在区间![]() 上是增函数,在
上是增函数,在![]() 上为减函数,
上为减函数,
又![]() ,
,
∴![]() .
.
(2)![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①若![]() ,令
,令![]() ,得极值点
,得极值点![]() ,
,
当![]() ,即
,即![]() 时,在
时,在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ,此时
,此时![]() 在区间
在区间![]() 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有![]() ,不合题意;
,不合题意;
当![]() ,即
,即![]() 时,同理可知,
时,同理可知,![]() 在区间
在区间![]() 上,有
上,有![]() ,也不合题意;
,也不合题意;
②若![]() ,则有
,则有![]() ,此时在区间
,此时在区间![]() 上恒有
上恒有![]() ,从而
,从而![]() 在区间
在区间![]() 上是减函数;
上是减函数;
要使![]() 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足![]() ,由此求得
,由此求得![]() 的范围是
的范围是![]() .
.
综合①②可知,当![]() 时,对
时,对![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() ,若对于任意的m,
,若对于任意的m,![]() 有
有![]() .
.
(1)判断函数的单调性(不要求证明);
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
,![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
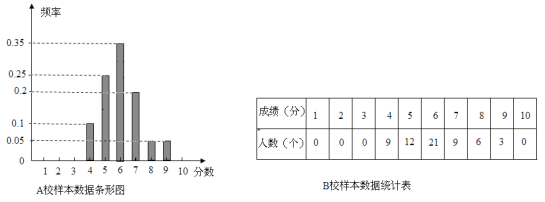
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在区间M=[a,b](a<b)使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间,给出下列四个函数:
①f(x)![]() ,②f(x)=x3,③f(x)=cos
,②f(x)=x3,③f(x)=cos![]() x,④f(x)=tanx
x,④f(x)=tanx
其中存在“稳定区间”的函数有( )
A.①②③B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1的方程为![]() ,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有微机![]() 台,分别放在
台,分别放在![]() 个房间,各房间开门钥匙互不相同.某期培训班有学员
个房间,各房间开门钥匙互不相同.某期培训班有学员![]() 人(
人(![]() ),每晚恰有
),每晚恰有![]() 人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这
人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这![]() 个学员,使得每晚不论哪
个学员,使得每晚不论哪![]() 个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com