
【题目】对于函数f(x),若存在区间M=[a,b](a<b)使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间,给出下列四个函数:
①f(x)![]() ,②f(x)=x3,③f(x)=cos
,②f(x)=x3,③f(x)=cos![]() x,④f(x)=tanx
x,④f(x)=tanx
其中存在“稳定区间”的函数有( )
A.①②③B.②③C.③④D.①④
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,动直线
两点,动直线![]() (
(![]() )与
)与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与圆交于
,与圆交于![]() 、
、![]() 两点(点
两点(点![]() 纵坐标大于点
纵坐标大于点![]() 纵坐标).
纵坐标).

(1)若![]() ,点
,点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标;
的坐标;
(2)若![]() ,
,![]() ,求直线
,求直线![]() 将圆分成的劣弧与优弧之比;
将圆分成的劣弧与优弧之比;
(3)若![]() ,设直线
,设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若圆![]() 的切线在
的切线在![]() 轴、
轴、![]() 轴上的截距相等,求切线方程;
轴上的截距相等,求切线方程;
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点为
向该圆引一条切线,切点为![]() ,且有
,且有![]() (
(![]() 为坐标原点),求使
为坐标原点),求使![]() 取得最小值时点
取得最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(acosx﹣sinx)![]() (a∈R),且f (
(a∈R),且f (![]() )
)![]() .
.
(1)求a的值;
(2)求f(x)的单调递增区间;
(3)求f(x)在区间[0,![]() ]上的最小值及对应的x的值.
]上的最小值及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
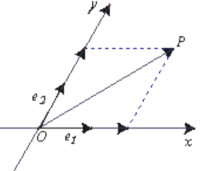
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆M:![]()
![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() 。
。
(1)求椭圆M的方程;
(2)已知![]() ,
,![]() 是椭圆M的下焦点,在椭圆M上是否存在点P,使
是椭圆M的下焦点,在椭圆M上是否存在点P,使![]() 的周长最大?若存在,请求出
的周长最大?若存在,请求出![]() 周长的最大值,并求此时
周长的最大值,并求此时![]() 的面积;若不存在,请说明理由。
的面积;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com