
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).
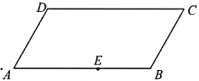
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
【答案】(1)![]() 是
是![]() 的中点;(2)
的中点;(2)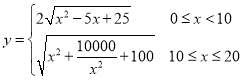 ;(3) 当
;(3) 当![]() ,
,![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.
【解析】
(1)由![]() 可知
可知![]() ,从而证明
,从而证明![]() 是
是![]() 的中点.
的中点.
(2)求出平行四边形的面积为![]() ,进而可求
,进而可求![]() ,从而用
,从而用![]() 可将
可将![]() 表示出来,利用余弦定理即可得到
表示出来,利用余弦定理即可得到![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当 ![]() ,由二次函数的性质可求最值;当
,由二次函数的性质可求最值;当![]() 时,由基本不等式可求最值.
时,由基本不等式可求最值.
解:(1)当点![]() 与点
与点![]() 重合时,由题设知,
重合时,由题设知,![]() .
.
于是![]() ,其中
,其中![]() 为平行四边形
为平行四边形![]() 边上的高.
边上的高.
得![]() ,即点
,即点![]() 是
是![]() 的中点.
的中点.
(2)因为点![]() 在线段
在线段![]() 上,所以
上,所以![]() .当
.当![]() 时,由(1)知
时,由(1)知
点![]() 在线段
在线段![]() 上.因为
上.因为![]()
所以![]() .
.
由![]() 得,
得,![]() .所以
.所以![]() 中,由余弦定理得
中,由余弦定理得
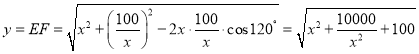 .
.
当![]() 时,点
时,点![]() 在线段
在线段![]() 上,由
上,由![]()
得![]() .当
.当![]() 时,
时,![]()
当![]() 时,
时,![]()
化简均为![]() .
.
综上,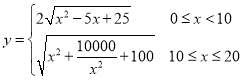 .
.
(3)当![]() 时,
时,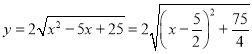 ,
,
于是当![]() 时,
时,![]() ,此时
,此时![]() .
.
当![]() 时,
时,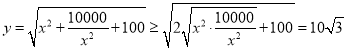
当且仅当![]() ,即
,即![]() 时,取等号
时,取等号
综上: 当![]() 距点
距点![]() ,
,![]() 距点
距点![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,一智能扫地机器人在A处发现位于它正西方向的B处和北偏东![]() 方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿
方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿![]() 路线清扫.已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务.
路线清扫.已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务.
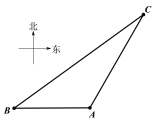
(1)B、C两处垃圾的距离是多少?(精确到0.1)
(2)智能扫地机器人此次清扫行走路线的夹角![]() 是多少?(用反三角函数表示)
是多少?(用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 且侧棱
且侧棱![]() 其中
其中![]() 为
为![]() 的
的![]() 交点.
交点.
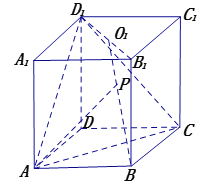
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)在线段![]() 上,是否存在一个点
上,是否存在一个点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直?若存在,求出线段
垂直?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1260 m,经测量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼游园工作,某单位设计了统计人数的数学模型![]() :以
:以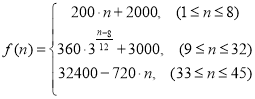 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以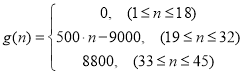 表示第
表示第![]() 个时刻离开园区的人数.设定以
个时刻离开园区的人数.设定以![]() 分钟为一个计算单位,上午
分钟为一个计算单位,上午![]() 点
点![]() 分作为第
分作为第![]() 个计算人数单位,即
个计算人数单位,即![]() ;
;![]() 点
点![]() 分作为第
分作为第![]() 个计算单位,即
个计算单位,即![]() ;依次类推,把一天内从上午
;依次类推,把一天内从上午![]() 点到晚上
点到晚上![]() 点
点![]() 分分成
分分成![]() 个计算单位(最后结果四舍五入,精确到整数).
个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天![]() 点至
点至![]() 点这一小时内,进入园区的游客人数
点这一小时内,进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]() 各为多少?
各为多少?
(2)假设当日园区游客总人数达到或超过![]() 万时,园区将采取限流措施.该单位借助该数学模型知晓当天
万时,园区将采取限流措施.该单位借助该数学模型知晓当天![]() 点(即
点(即![]() )时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
)时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() ,设
,设 .
.
(1)如果![]() 为奇函数,求实数
为奇函数,求实数![]() 、
、![]() 满足的条件;
满足的条件;
(2)在(1)的条件下,若函数![]() 在区间
在区间![]() 上为增函数,求
上为增函数,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() 恒有
恒有![]() 成立.证明:当
成立.证明:当![]() 时,
时,![]() 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com