【题目】设函数
，
.
（1）当
（
为自然对数的底数）时，求
的极小值；
（2）讨论函数
零点的个数.
【答案】（1）极小值
；
（2）①当
时，
无零点，
②当
或
时，有且仅有
个零点，
③当
时，有两个零点.
【解析】
试题（1）要求
的极小值，可以通过判断其单调性从而求得其极小值，对求导，可知
，再通过列表即可得当
时，
取得极小值
；（2）令
，可得
，因此要判断函数
的零点个数，可通过画出函数
的草图来判断，同样可以通过求导判断函数的单调性来画出函数图象的草图：
，通过列表可得到
的单调性，作出
的图象，进而可得
①当
时，
无零点，②当或
时，有且仅有个零点，
③当
时，有两个零点.
试题解析：（1）当
时，
，其定义域为
，
，
令
，，
|
|
|
|
|
|
|
|
|
| 极小值 |
|
故当时，取得极小值；
（2）
，其定义域为，
令
，得，
设
，其定义域为.则的零点为与
的交点，
，
|
|
|
|
|
|
|
|
|
| 极大值 |
|
故当
时，取得最大值
作出的图象，可得
①当时，无零点，
②当或时，有且仅有个零点，
③当时，有两个零点.
科目：高中数学 来源： 题型：
【题目】下列说法错误的是（ ）
A.命题“若
，则
”的逆否命题是“若
，则
”
B.“
”是“
”的充分不必要条件
C.若
为假命题，则
、
均为假命题
D.命题：“
，使得
”，则非：“
，
”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个正方形花圃被分成5份．
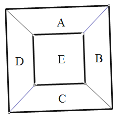
（1）若给这5个部分种植花，要求相邻两部分种植不同颜色的花，己知现有红、黄、蓝、绿4种颜色不同的花，求有多少种不同的种植方法?
（2）若将6个不同的盆栽都摆放入这5个部分，且要求每个部分至少有一个盆栽，问有多少种不同的放法?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列判断正确的是（ ）
A.若随机变量
服从正态分布
，
，则
；
B.已知直线
平面
，直线
平面
，则“
”是“
”的必要不充分条件；
C.若随机变量服从二项分布：
，则
；
D.已知直线
经过点
，则
的取值范围是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值
与销售单价
之间的关系,经统计得到如下数据：
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；
（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？
参考公式：对一组数据
,
，····
,其回归直线
的斜率和截距最小二乘估计分别为：
,
.
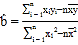参考数据：
,
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某小型企业甲产品生产的投入成本x（单位：万元）与产品销售收入y（单位：万元）存在较好的线性关系，下表记录了最近5次该产品的相关数据.
x（万元） | 3 | 5 | 7 | 9 | 11 |
y（万元） | 8 | 10 | 13 | 17 | 22 |
（1）求y关于x的线性回归方程；
（2）根据（1）中的回归方程，判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大（毛利率
）？
相关公式：
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
已知函数
是奇函数，的定义域为
．当
时， 
．(e为自然对数的底数)．
(1)若函数在区间
上存在极值点，求实数
的取值范围；
(2)如果当x≥1时，不等式
恒成立，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法：
①对于独立性检验，
的值越大，说明两事件相关程度越大；
②以模型
去拟合一组数据时，为了求出回归方程，设
，将其变换后得到线性方程
，则
，
的值分别是
和0.3；
③已知随机变量
，若
，则
（
）的值为
；
④通过回归直线
及回归系数
，可以精确反映变量的取值和变化趋势．
其中错误的选项是（ ）
A.①B.②C.③D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
