
分析 利用参数分离法进行转化,求函数的最值即可.
解答 解:∵当a∈[$\frac{1}{3}$,3],函数f(x)在[$\frac{1}{4}$,1]上为减函数,
∴若f(x0)>3,
则f(x0)=$\frac{a}{\sqrt{{x}_{0}}}$+b>3成立,
即b>3-$\frac{a}{\sqrt{{x}_{0}}}$成立即可,
设y=3-$\frac{a}{\sqrt{{x}_{0}}}$,则函数为增函数,
则当a=$\frac{1}{3}$,x0=$\frac{1}{4}$时,函数取得最小值为y=3-$\frac{\frac{1}{3}}{\sqrt{\frac{1}{4}}}$=3-$\frac{\frac{1}{3}}{\frac{1}{2}}$=3-$\frac{2}{3}$=$\frac{7}{3}$,
即b>$\frac{7}{3}$即可,
故答案为:($\frac{7}{3}$,+∞)
点评 本题主要考查函数恒成立问题,利用参数分离法转化求函数的最值是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | a≤-1 | C. | a≥1 | D. | a≥-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
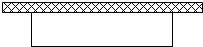 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com