
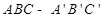 的正(主)视图和侧(左)视图如图所示. 设
的正(主)视图和侧(左)视图如图所示. 设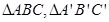 的中心分别是
的中心分别是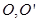 ,现将此三棱柱绕直线
,现将此三棱柱绕直线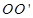 旋转,射线
旋转,射线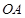 旋转所成的角为
旋转所成的角为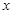 弧度(
弧度(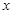 可以取到任意一个实数),对应的俯视图的面积为
可以取到任意一个实数),对应的俯视图的面积为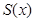 ,则函数
,则函数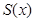 的最大值为 ;最小正周期为 .
的最大值为 ;最小正周期为 . 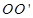 旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,
旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,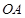 旋转所成的角为正角,顺时针方向旋转时,
旋转所成的角为正角,顺时针方向旋转时,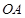 旋转所成的角为负角.
旋转所成的角为负角.科目:高中数学 来源:不详 题型:解答题
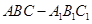 的各棱长都是4,
的各棱长都是4, 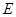 是
是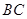 的中点,动点
的中点,动点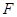 在侧棱
在侧棱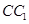 上,且不与点
上,且不与点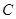 重合.
重合.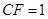 时,求证:
时,求证: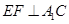 ;
;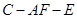 的大小为
的大小为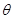 ,求
,求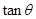 的最小值.
的最小值.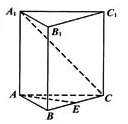
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, " AA ="2, " E、E
="2, " E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
 //平面FCC
//平面FCC ;
; -C的余弦值。
-C的余弦值。 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
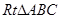 中,
中,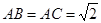 ,
,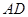 斜边
斜边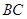 上的高,以
上的高,以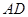 为折痕,将
为折痕,将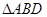 折 起,使
折 起,使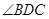 为直角。
为直角。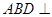 平面
平面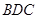 ;(2)求证:
;(2)求证: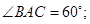
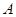 到平面
到平面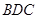 的距离;(4) 求点
的距离;(4) 求点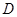 到平面
到平面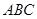 的距离;
的距离; 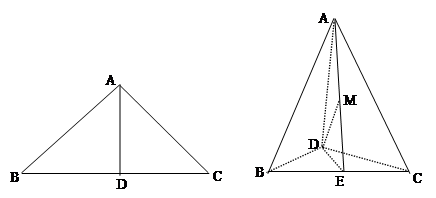
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是圆柱的母线,
是圆柱的母线, 是圆柱底面圆的直径,
是圆柱底面圆的直径, 是底面圆周上异于
是底面圆周上异于 的任意一点,
的任意一点,
 平面
平面 ;
; 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
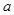 和两个平面
和两个平面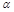 ,β,给出下列四个命题:
,β,给出下列四个命题: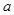 ∥
∥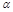 ,则
,则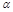 内的任何直线都与
内的任何直线都与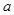 平行;
平行;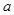 ⊥α,则
⊥α,则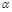 内的任何直线都与
内的任何直线都与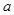 垂直;
垂直;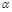 ∥β,则β内的任何直线都与
∥β,则β内的任何直线都与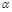 平行;
平行;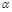 ⊥β,则β内的任何直线都与
⊥β,则β内的任何直线都与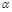 垂直.
垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com