
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
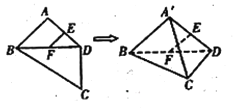
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
科目:高中数学 来源: 题型:
【题目】在三棱锥P-ABC中,三条侧棱PA、PB、PC两两垂直,且![]() ,
,![]() ,又M是底面ABC内一点,则M到三个侧面的距离的平方和的最小值是________.
,又M是底面ABC内一点,则M到三个侧面的距离的平方和的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() 与双曲线
与双曲线![]() 有相同的渐近线,且双曲线C过点
有相同的渐近线,且双曲线C过点![]() .
.
(1)若双曲线C的左、右焦点分别为![]() ,
,![]() ,双曲线C上有一点P,使得
,双曲线C上有一点P,使得![]() ,求△
,求△![]() 的面积;
的面积;
(2)过双曲线C的右焦点![]() 作直线l与双曲线右支交于A,B两点,若△
作直线l与双曲线右支交于A,B两点,若△![]() 的周长是
的周长是![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设λ是正实数,(1+λx)20的二项展开式为a0+a1x+a2x2+…+a20x20,其中a0,a1,…,a20 ,…,均为常数
(1)若a3=12a2,求λ的值;
(2)若a5≥an对一切n∈{0,1,…,20}均成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每千克![]() 元,成本为每千克
元,成本为每千克![]() 元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失
元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失![]() 元.根据以往的市场调查,将市场日需求量(单位:千克)按
元.根据以往的市场调查,将市场日需求量(单位:千克)按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图的频率分布直方图.
进行分组,得到如图的频率分布直方图.

(Ⅰ)未来连续三天内,连续两天该种鲜钱的日需求量不低于![]() 千克,而另一天的日需求量低于
千克,而另一天的日需求量低于![]() 千克的概率;
千克的概率;
(Ⅱ)在频率分布直方图的日需求量分组中,以各组区间的中点值代表该组的各个值,并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货![]() 千克,记经销商每日利润为
千克,记经销商每日利润为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中有高一新生500名,分成水平相同的![]() 两类教学实验,为对比教学效果,现用分层抽样的方法从
两类教学实验,为对比教学效果,现用分层抽样的方法从![]() 两类学生中分别抽取了40人,60人进行测试
两类学生中分别抽取了40人,60人进行测试
(1)求该学校高一新生![]() 两类学生各多少人?
两类学生各多少人?
(2)经过测试,得到以下三个数据图表:
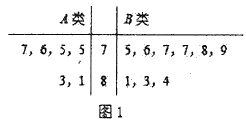
图1:75分以上![]() 两类参加测试学生成绩的茎叶图
两类参加测试学生成绩的茎叶图
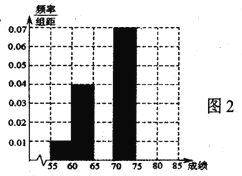
图2:100名测试学生成绩的频率分布直方图
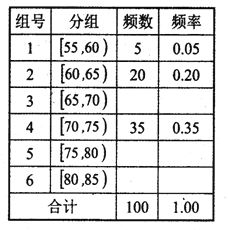
下图表格:100名学生成绩分布表:
①先填写频率分布表中的六个空格,然后将频率分布直方图(图2)补充完整;
②该学校拟定从参加考试的79分以上(含79分)的![]() 类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图茎叶图:

![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
![]() 完成下面的列联表,并根据列联表判断是否有
完成下面的列联表,并根据列联表判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | |
第一阶段 | ||
第二阶段 |
附:![]()
|
|
|
|
k |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 点
点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 为实数).
为实数).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求证:直线![]() 与直线
与直线![]() 不可能垂直.
不可能垂直.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com