
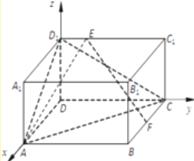
【题目】如图,在长方体![]() 中,
中,![]() 点
点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 为实数).
为实数).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求证:直线![]() 与直线
与直线![]() 不可能垂直.
不可能垂直.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)建立如图所示的空间直角坐标系,写出相应点的坐标,算出相应向量的坐标,利用垂直向量的数量积等于零的方法建立方程组,算出平面对应的法向量,之后应用平面的法向量所成角的余弦值求得二面角的余弦值;’
(2)当![]() 时,可得E,F的坐标,从而求得
时,可得E,F的坐标,从而求得![]() 的坐标,进而算出
的坐标,进而算出![]() 的余弦值,再由其为锐角,结合直线与平面所成角的定义,即可算出直线与平面所成角的正弦值的大小;
的余弦值,再由其为锐角,结合直线与平面所成角的定义,即可算出直线与平面所成角的正弦值的大小;
(3)假设直线![]() 与直线
与直线![]() 垂直,根据向量的数量积等于零,建立关于
垂直,根据向量的数量积等于零,建立关于![]() 的等量关系式,化简可得
的等量关系式,化简可得![]() ,由根的判别式小于零得该方程无解,从而得到假设不成立,从而得到原结论成立.
,由根的判别式小于零得该方程无解,从而得到假设不成立,从而得到原结论成立.
详解:(1)如图所示,建立空间直角坐标系![]() .
.
则![]()
![]()
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() .即
.即![]() .令
.令![]() ,则
,则![]() .
.
∴平面![]() 的一个法向量
的一个法向量![]() .又平面
.又平面![]() 的一个法向量为
的一个法向量为![]() .
.
故![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() .
.
(2)当λ =![]() 时,E(0,1,2),F(1,4,0),
时,E(0,1,2),F(1,4,0),![]() .
.
所以![]() .
.
因为 ![]() ,所以
,所以![]() 为锐角,
为锐角,
从而直线EF与平面![]() 所成角的正弦值的大小为
所成角的正弦值的大小为![]() .
.
(3)假设![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .化简得
.化简得![]() .
.
该方程无解,所以假设不成立,即直线![]() 不可能与直线
不可能与直线![]() 不可能垂直.
不可能垂直.


科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.
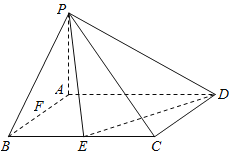
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级共派出![]() 个男生和
个男生和![]() 个女生参加学校运动会的入场仪式,其中男生倪某为领队.入场时,领队男生倪某必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生倪某为领队.入场时,领队男生倪某必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有![]() 种排法;入场后,又需从男生(含男生倪某)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生倪某)和女生中各选一名代表到主席台服务,共有![]() 种选法.(1)试求
种选法.(1)试求![]() 和
和![]() ; (2)判断
; (2)判断![]() 和
和![]() 的大小(
的大小(![]() ),并用数学归纳法证明.
),并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
A.![]() +
+ ![]() =1
=1
B.![]() +
+ ![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() +
+ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com