Question

【题目】已知函数在与时都取得极值．

（1）求的值与函数的单调区间；

（2）若对,不等式恒成立，求的取值范围．

Answer 1

【答案】解：（1）……………………2分

由，

……………………3分

得……………………5分

（2），

当时，为极大值，……………………6分

而，则为最大值，……………………8分

要使

恒成立，则只需要，……………………10分

得……………………12分

【解析】

（1）求出f（x），由题意得f（）＝0且f（1）＝0联立解得与b的值，然后把、b的值代入求得f（x）及f（x），讨论导函数的正负得到函数的增减区间；

（2）根据（1）函数的单调性，由于x∈[﹣1，2]恒成立求出函数的最大值为f（2），代入求出最大值，然后令f（2）＜c2列出不等式，求出c的范围即可．

（1），f（x）＝3x2+2ax+b

由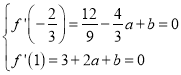解得，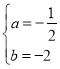

f（x）＝3x2﹣x﹣2＝（3x+2）（x﹣1），函数f（x）的单调区间如下表：

x	（﹣∞,）		（，1）	1	（1，+∞）
f（x）	+	0	﹣	0	+
f（x）		极大值		极小值

所以函数f（x）的递增区间是（﹣∞，）和（1，+∞），递减区间是（，1）．

（2）因为，根据（1）函数f（x）的单调性，

得f（x）在（﹣1，）上递增，在（，1）上递减，在（1，2）上递增，

所以当x时，f（x）为极大值，而f（2）＝，所以f（2）＝2+c为最大值．

要使f（x）＜对x∈[﹣1，2]恒成立，须且只需＞f（2）＝2+c．

解得c＜﹣1或c＞2．