
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
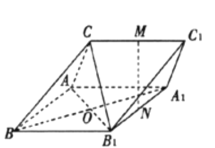
(1)证明:直线![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)设![]() 与
与![]() 交于点
交于点![]() ,通过证明
,通过证明![]() 是平行四边形证得
是平行四边形证得![]() ,得线面平行;
,得线面平行;
(2)证明![]() 两两垂直,然后以
两两垂直,然后以![]() 为
为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,写出各点坐标,求出两平面的法向量,利用法向量夹角的余弦得二面角的余弦.
,写出各点坐标,求出两平面的法向量,利用法向量夹角的余弦得二面角的余弦.
证明:(1)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,
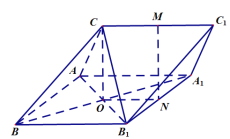
因为四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)因为![]() ,所以平行四边形
,所以平行四边形![]() 是菱形,所以
是菱形,所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
又![]() ,且
,且![]() 是
是![]() 的中点,所以
的中点,所以![]() .又因为
.又因为![]() ,
,
所以![]() ,
,
所以![]() ,故
,故![]() ,从而
,从而![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系![]() ,
,
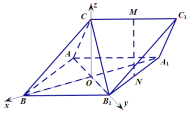
设![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() 是等边三角形,所以
是等边三角形,所以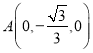 ,
,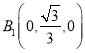 ,
,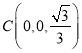 ,
,![]() .
.
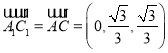 ,
,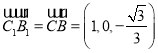 .
.
因为![]() ,
,![]() ,
,![]() 两两垂直,所以
两两垂直,所以![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
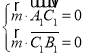 ,即
,即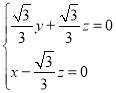 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值为
所成的角(锐角)的余弦值为![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,现沿对角线
,现沿对角线![]() 将
将![]() 折起,使点A到达点P,点M,N分别在直线
折起,使点A到达点P,点M,N分别在直线![]() ,
,![]() 上,且A,B,M,N四点共面.
上,且A,B,M,N四点共面.
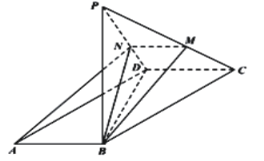
(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小为
平面角大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与直线
与直线![]() 分别与椭圆
分别与椭圆![]()
![]() 交于点
交于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,是否存在经过原点,且以
两点,是否存在经过原点,且以![]() 为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程(结果保留两位小数);
的回归直线方程(结果保留两位小数);
(2)现从2012—2018年这7年中抽出三年进行调查,记![]() 年利润增长-投资金额,设这三年中
年利润增长-投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: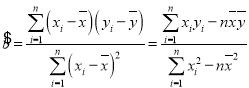 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py经过点(2,1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为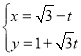 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 是椭圆右顶点,已知直线
是椭圆右顶点,已知直线![]() 的斜率为
的斜率为![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() .
.

(1)求椭圆的方程;
(2)若椭圆上有两点![]() ,使
,使![]() 的平分线垂直
的平分线垂直![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com