
分析 根据辅助角公式,化简函数得y=2sin(x+$\frac{π}{3}$),从而得出平移后的图象对应的函数为y=2sin(x+$\frac{π}{3}$-φ).由平移后的图象关于原点对称,根据正弦函数的图象与性质得到$\frac{π}{3}$-φ=kπ(k∈Z),再取k=0得到φ的最小正值为$\frac{π}{3}$.
解答 解:y=sinx+$\sqrt{3}$cosx=2(sinxcos$\frac{π}{3}$+cosxsin$\frac{π}{3}$)=2sin(x+$\frac{π}{3}$).
将函数的图象向右平移φ(φ>0)个单位长度后,得到y=2sin[(x-φ)+$\frac{π}{3}$]=2sin(x+$\frac{π}{3}$-φ)的图象.
∵平移后得到的图象关于坐标原点对称,
∴$\frac{π}{3}$-φ=kπ(k∈Z),可得φ=$\frac{π}{3}$-kπ(k∈Z),
取k=0,得到φ的最小正值为$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题给出三角函数表达式,已知函数图象右移φ个单位个图象关于原点对称,求平移的最小长度.着重考查了三角恒等变换公式、正弦函数的图象与性质和函数图象平移公式等知识,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
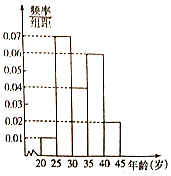 今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.
在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有两个个体与其它个体被抽到的概率不相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com