
分析 (1)由直线l1与圆相切,则圆心到直线的距离等于半径,求得直线方程,注意分类讨论;
(2)分别联立相应方程,求得M,N的坐标,再求|AM|•|AN|.
解答 解:(1)①当直线斜率存在时,设直线的斜率为k,则直线方程为:y-0=k(x-1),
即kx-y-k=0.因为直线与圆相切,所以$d=\frac{{|{3k-4-k}|}}{{\sqrt{{k^2}+1}}}=2$,解得$k=\frac{3}{4}$….3
所以直线方程是:3x-4y-3=0.
②当直线斜率不存在时,直线为x=1,满足题意.
综上可知:直线的方程是3x-4y-3=0或x=1…..6
(2)因为直线与圆相交,所以斜率存在,设斜率为k,则直线l:y=k(x-1)
联立$\left\{\begin{array}{l}y=k({x-1})\\ x+2y+2=0\end{array}\right.$得$\left\{\begin{array}{l}x=\frac{2k-2}{1+2k}\\ y=\frac{-3k}{1+2k}\end{array}\right.$所以$N({\frac{2k-2}{1+2k},\frac{-3k}{1+2k}})$…8
因为M是PQ的中点,所以CM⊥PQ.设直线CM的方程:$y-4=-\frac{1}{k}({x-3})$
联立$\left\{\begin{array}{l}y-4=-\frac{1}{k}({x-3})\\ y=k({x-1})\end{array}\right.$得$M({\frac{{{k^2}+4k+3}}{{{k^2}+1}},\frac{{4{k^2}+2k}}{{{k^2}+1}}})$.…10
所以$\overrightarrow{AM}=({\frac{4k+2}{{{k^2}+1}},\frac{{4{k^2}+2k}}{{{k^2}+1}}}),\overrightarrow{AN}=({\frac{-3}{1+2k},\frac{-3k}{1+2k}})$
所以$\overrightarrow{AM}•\overrightarrow{AN}=-6$,因为$\overrightarrow{AM}•\overrightarrow{AN}=-|{AM}|•|{AN}|$$|{AM}|•|{AN}|=-\overrightarrow{AM}•\overrightarrow{AN}=6$….12
点评 本题主要考查圆的标准方程,简单几何性质,直线与圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.


科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ②④ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | (1,3) | C. | [-3,-1] | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
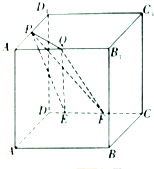 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12π | B. | 4$\sqrt{3}π$ | C. | 12$\sqrt{3}π$ | D. | $\frac{4}{3}$$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {2,4} | C. | {2,4,5} | D. | {1,2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com