
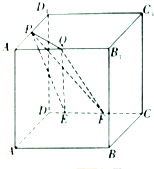
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.分析 对4个结论分别进行判断,即可得出结论.
解答 解:①中,∵平面QEF也就是平面A1B1CD,既然P和平面QEF都是固定的,∴P到平面A1B1CD的距离是定值,∴点P到平面QEF的距离为定值;
②中,∵△QEF的面积是定值(∵EF定长,Q到EF的距离就是Q到CD的距离也为定长,即底和高都是定值),再根据①的结论P到平面QEF的距离也是定值,∴三棱锥的高也是定值,于是体积固定,∴三棱锥P-QEF的体积是定值;
③中,∵Q是动点,E,F也是动点,推不出定值的结论,∴直线PQ与平面PEF所成的角不是定值;
④中,由图,平面QEF也就是平面A1B1CD,又∵平面PEF即为平面PCD,∴二面角P-EF-Q的大小为定值.
故答案为:①②④.
点评 本题考查的知识点是直线与平面所成的角,二面角,棱锥的体积及点到平面的距离,其中两线平行时,一条线的上的点到另一条直线的距离相等,线面平行时直线上到点到平面的距离相等,平面平行时一个平面上的点到另一个平面的距离相等是解答本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{11}$ | B. | $\frac{9}{22}$ | C. | $\frac{7}{13}$ | D. | $\frac{9}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.
如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(面积) | 4 | 6 | 9 | 7 | 8 | 8 |
| y(销售额) | 3 | 5 | 6 | 4 | 5 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com