
分析 先求出f(x)+f(-x)=2,f(0)=1,由此能求出f(-3)+f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值.
解答 解:∵函数$f(x)=\frac{2}{{{3^x}+1}}+sinx$,
∴f(x)+f(-x)=$\frac{2}{{3}^{x}+1}+sinx$+$\frac{2}{{3}^{-x}+1}+sin(-x)$
=$\frac{2}{{3}^{x}+1}+sinx$+$\frac{2×{3}^{x}}{1+{3}^{x}}$-sinx
=2,
f(0)=$\frac{2}{{3}^{0}+1}+sin0=1$,
∴f(-3)+f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)
=[f(-3)+f(3)]+[f(-2)+f(2)]+[f(-1)+f(1)]+f(0)
=2+2+2+1
=7.
故选为:7.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
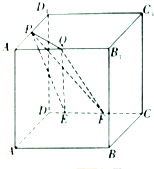 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12π | B. | 4$\sqrt{3}π$ | C. | 12$\sqrt{3}π$ | D. | $\frac{4}{3}$$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {2,4} | C. | {2,4,5} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{{x}^{′}=\frac{1}{2}x}\\{{y}^{′}=2y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x′=\frac{1}{3}x}\\{y′=2y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x′=2x}\\{y′=\frac{1}{2}y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x′=x}\\{y′=2y}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com