
| x(面积) | 4 | 6 | 9 | 7 | 8 | 8 |
| y(销售额) | 3 | 5 | 6 | 4 | 5 | 7 |
分析 (1)根据所给的数据先做出数据的平均数,即样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程;
(2)将x=10代入线性回归方程,可得对应的年销售额.
解答 解:(1)由题意得$\sum_{i=1}^6{x_i}{y_i}=4×3+6×5+9×6+7×4+8×5+8×7=220$------(2分)${\sum_{i=1}^6{x_i}^2}=16+36+81+49+64+64=310$------(4分)$\overline x=\frac{4+6+9+7+8+8}{6}=7$------(5分)$\overline y=\frac{3+5+6+4+5+7}{6}=5$------(6分)
∴$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$=0.625------(8分)
$\widehata=\overline y-\widehatb\overline x$=0.625------(9分)
∴回归直线方程为$\widehaty=0.625x+0.625$------(10分)
(2)将x=10代入得$\widehaty=6.875$------(12分)
答:回归直线方程为$\widehaty=0.625x+0.625$;一个拥有一万平方米的商店来说,它的年销售额约为687.5万元------(14分)
点评 本题考查求线性回归方程,是一个运算量比较大的问题,解题时注意平均数的运算不要出错,注意系数的求法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | (1,3) | C. | [-3,-1] | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
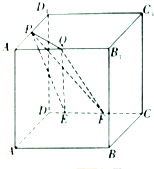 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12π | B. | 4$\sqrt{3}π$ | C. | 12$\sqrt{3}π$ | D. | $\frac{4}{3}$$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com