
 如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.
如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.分析 (1)推导出PA⊥BC,BC⊥AB,从而BC⊥面PAB,进而BC⊥AE,再由AE⊥PB,能证明AE⊥平面PBC.
(2)在面PAB内过E做EH∥PA,交AB于H,由VC-AED=VE-ACD,能求出三棱锥C-AED的体积.
解答 证明:(1)∵PA⊥平面ABCD,BC?面ABCD,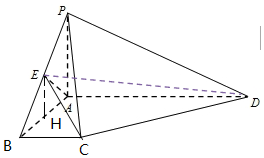
∴PA⊥BC,
又∠ABC=90°,∴BC⊥AB,
∵PA∩AB=A,∴BC⊥面PAB,
∵AE?平面PAB,∴BC⊥AE,
又AB=PA=1,E是PB的中点.∴AE⊥PB,
∵PB∩BC=B,∴AE⊥平面PBC.
解:(2)在面PAB内过E做EH∥PA,交AB于H,
∵PA⊥平面ABCD,∴EH⊥平面ABCD,
∴三棱锥C-AED的体积${V_{C-AED}}={V_{E-ACD}}=\frac{1}{3}•{S_{△ACD}}•EH=\frac{1}{4}$.
点评 本题考查线面垂直的证明,考查二棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
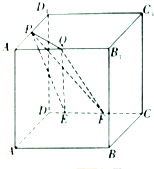 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则以下四个值中为定值的编号是①②④.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
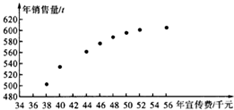 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千克)对年消售量y(单位:t)和年利润z(单位:千克)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千克)对年消售量y(单位:t)和年利润z(单位:千克)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12π | B. | 4$\sqrt{3}π$ | C. | 12$\sqrt{3}π$ | D. | $\frac{4}{3}$$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.4米 | B. | 3.0米 | C. | 3.6米 | D. | 4.5米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com