
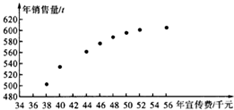
 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千克)对年消售量y(单位:t)和年利润z(单位:千克)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千克)对年消售量y(单位:t)和年利润z(单位:千克)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
分析 (Ⅰ)根据散点图,即可判断出,
(Ⅱ)先建立中间量w=$\sqrt{x}$,建立y关于w的线性回归方程,根据公式求出w,问题得以解决;
(Ⅲ)(i)年宣传费x=49时,代入到回归方程,计算即可,
(ii)求出预报值得方程,根据函数的性质,即可求出.
解答 解:(Ⅰ)由散点图可以判断,y=c+d $\sqrt{x}$,适宜作为年销售量y关于年宣传费x的回归方程类型;
(Ⅱ)令w=$\sqrt{x}$,先建立y关于w的线性回归方程,由于$\widehat{d}$=$\frac{108.6}{1.6}$68,
$\widehat{c}$=$\widehat{y}$-$\widehat{d}$w=563-68×6.8=100.6,
∴y关于w的线性回归方程为$\widehat{y}$=100.6+68w,
∴y关于x的回归方程为$\widehat{y}$=100.6+68$\sqrt{x}$,
(Ⅲ)(i)由(Ⅱ)知,当x=49时,年销售量y的预报值$\widehat{y}$=100.6+68$\sqrt{49}$=576.6,
年利润z的预报值$\widehat{z}$=576.6×0.2-49=66.32,
(ii)根据(Ⅱ)的结果可知,年利润z的预报值$\widehat{z}$=0.2(100.6+68$\sqrt{x}$)-x=-x+13.6$\sqrt{x}$+20.12,
当$\sqrt{x}$=$\frac{13.6}{2}$=6.8时,年利润的预报值最大.
点评 本题主要考查了线性回归方程和散点图的问题,考查线性回归方程的求法,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | ($\frac{1}{2}$,2) | C. | [1,$\sqrt{2}$) | D. | ($\frac{\sqrt{2}}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.
如图,PA⊥平面ABCD,AD∥BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直线y=-x+1与椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相交于A、B两点.
已知直线y=-x+1与椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相交于A、B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com