
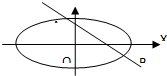
 ��ֱ֪��y=-x+1����Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ཻ��A��B���㣮
��ֱ֪��y=-x+1����Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ཻ��A��B���㣮���� ��1��$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$��a2=b2+c2����Ϊ��$a=\sqrt{3}c$��b=$\sqrt{2}$c����Բ�ķ���Ϊ��$\frac{{x}^{2}}{3{c}^{2}}+\frac{{y}^{2}}{2{c}^{2}}$=1���ɵ�2x2+3y2=6c2����A��x1��y1����B��x2��y2����ֱ�߷�������Բ����������Ϊ��5x2-6x+3-6c2=0������|AB|=$\sqrt{2[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\frac{{8\sqrt{3}}}{5}$��������ɵó���
��2����A��x1��y1����B��x2��y2����ֱ�߷�������Բ����������Ϊ����b2+a2��x2-2a2x+a2-a2b2=0���Ѹ���ϵ���Ĺ�ϵ����$\overrightarrow{OA}$$•\overrightarrow{OB}$=x1x2+y1y2=x1x2+��-x1+1����-x2+1��=2x1x2-��x1+x2��+1=0����������ó���
��� �⣺��1����$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$��a2=b2+c2����Ϊ��$a=\sqrt{3}c$��b=$\sqrt{2}$c��
����Բ�ķ���Ϊ��$\frac{{x}^{2}}{3{c}^{2}}+\frac{{y}^{2}}{2{c}^{2}}$=1���ɵ�2x2+3y2=6c2��
��A��x1��y1����B��x2��y2��������$\left\{\begin{array}{l}{y=-x+1}\\{2{x}^{2}+3{y}^{2}=6{c}^{2}}\end{array}\right.$������5x2-6x+3-6c2=0��
��x1+x2=$\frac{6}{5}$��x1•x2=$\frac{3-6{c}^{2}}{5}$��
��|AB|=$\sqrt{2[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2[\frac{36}{25}-\frac{4��3-6{c}^{2}��}{5}]}$=$\frac{{8\sqrt{3}}}{5}$�����c2=1��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1��
��2����A��x1��y1����B��x2��y2��������$\left\{\begin{array}{l}{y=-x+1}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$��������b2+a2��x2-2a2x+a2-a2b2=0��
��=4a4-4��b2+a2����a2-a2b2����0��
��x1+x2=$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}$��x1x2��=$\frac{{a}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$��
��$\overrightarrow{OA}$$•\overrightarrow{OB}$=x1x2+y1y2=x1x2+��-x1+1����-x2+1��=2x1x2-��x1+x2��+1
=2��$\frac{{a}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$-$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}$+1=0��
��a2+b2-2a2b2=0��
��$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2{a}^{2}-1}$��
��e��[$\frac{1}{2}$��$\frac{{\sqrt{2}}}{2}$]����${e}^{2}=\frac{{c}^{2}}{{a}^{2}}$=1-$\frac{{a}^{2}}{{b}^{2}}$=1-$\frac{1}{2{a}^{2}-1}$��$[\frac{1}{4}��\frac{1}{2}]$��
��$\frac{7}{6}$��a2��$\frac{3}{2}$��
��$\frac{\sqrt{42}}{6}$��a��$\frac{\sqrt{6}}{2}$��
��2a��$[\frac{\sqrt{42}}{3}��\sqrt{6}]$��
����Բ�ij��᳤�����ֵ��$\sqrt{6}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ���ཻ�ҳ����⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��б�ʴ�ֱ���������Ĺ�ϵ����������������������������������⣮


 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
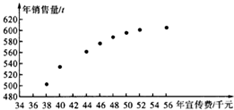 ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧ�ˣ�����������y����λ��t����������z����λ��ǧ�ˣ���Ӱ�죬�Խ�8���������xi����������yi��i=1��2��3��..8���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ��
ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧ�ˣ�����������y����λ��t����������z����λ��ǧ�ˣ���Ӱ�죬�Խ�8���������xi����������yi��i=1��2��3��..8���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ��| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$��xi-$\overline{x}$��2 | $\sum_{i=1}^{8}$��wi-$\overline{w}$��2 | $\sum_{i=1}^{8}$��xi-$\overline{x}$����yi-$\overline{y}$�� | $\sum_{i=}^{8}$��wi-$\overline{w}$����yi-$\overline{y}$�� |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.4�� | B�� | 3.0�� | C�� | 3.6�� | D�� | 4.5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4��14�� | B�� | ��6��6�� | C�� | ��3��18�� | D�� | ��10��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com