
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
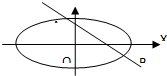 已知直线y=-x+1与椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相交于A、B两点.
已知直线y=-x+1与椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第1组 | 2 | 2 | 第13组 | 5 | 6 | 第25组 | 2 | 6 |
| 第2组 | 6 | 5 | 第14组 | 1 | 4 | 第62组 | 6 | 3 |
| 第3组 | 1 | 3 | 第15组 | 2 | 3 | 第27组 | 6 | 6 |
| 第4组 | 5 | 3 | 第16组 | 5 | 2 | 第28组 | 1 | 2 |
| 第5组 | 5 | 2 | 第17组 | 1 | 6 | 第29组 | 6 | 1 |
| 第6组 | 4 | 5 | 第18组 | 4 | 6 | 第30组 | 4 | 1 |
| 第7组 | 3 | 4 | 第19组 | 3 | 1 | 第31组 | 3 | 6 |
| 第8组 | 6 | 5 | 第20组 | 4 | 2 | 第32组 | 4 | 3 |
| 第9组 | 3 | 4 | 第21组 | 3 | 3 | 第33组 | 5 | 6 |
| 第10组 | 6 | 4 | 第22组 | 4 | 4 | 第34组 | 1 | 6 |
| 第11组 | 1 | 2 | 第23组 | 6 | 2 | 第35组 | 4 | 2 |
| 第12组 | 1 | 5 | 第24组 | 5 | 2 | 第36组 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
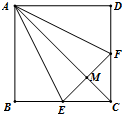 如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )
如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )| A. | PM⊥△AEF所在平面 | B. | AM⊥△PEF所在平面 | C. | PF⊥△AEF所在平面 | D. | AP⊥△PEF所在平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2-$\sqrt{7}$,1,3} | B. | {2-$\sqrt{7}$,1,3} | C. | {-3,-1,1,3} | D. | {1,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com