
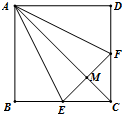
 如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )
如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )| A. | PM⊥△AEF所在平面 | B. | AM⊥△PEF所在平面 | C. | PF⊥△AEF所在平面 | D. | AP⊥△PEF所在平面 |
分析 本题为折叠问题,分析折叠前与折叠后位置关系、几何量的变与不变,可得PA、PE、PF三者相互垂直,根据线面垂直的判定定理,可判断AP与平面PEF的垂直,从而得出结论.
解答 
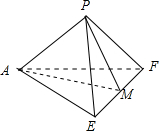 解:在折叠过程中,根据折叠前、后AP⊥EP,AP⊥PF不变,
解:在折叠过程中,根据折叠前、后AP⊥EP,AP⊥PF不变,
∴AP⊥平面EFP,故D满足条件;
∵过点A只有一条直线与平面EFP垂直,∴B不正确;
∵PM不垂直于AM,AM?平面AEF,故PM不垂直于平面AEF,故A不正确;
AM⊥EF,EF⊥AP,∴EF⊥平面HAG,∴平面HAG⊥AEF,
过H作直线垂直于平面AEF,则该垂线一定在平面PAM内,而PF不在平面PAM内,
故C不正确,
故选:D.
点评 本题主要考查直线和平面垂直的判定,一般利用线线?线面?面面,垂直关系的相互转化判断,折叠问题,属于中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | α丄γ,m∥β | B. | α 丄γ,l丄m | C. | m∥β,l丄m | D. | α∥β,γ丄β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |PF1|+|PF2|<4 | B. | |PF1|+|PF2|>4 | C. | |PF1|+|PF2|<6 | D. | |PF1|+|PF2|>6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com