
分析 (1)利用直接法,可得点P的轨迹方程,并指出是什么图形;
(2)利用圆心到此直线的距离小于半径,求实数k的取值范围;
(3)由$\left\{\begin{array}{l}y=kx-1\\{x^2}+{y^2}-4x-6y+9=0\end{array}\right.$消去y:(1+k2)x2-4(2k+1)x+16=0,利用韦达定理及向量数量积运算可得结论.
解答 解:(1)设动点P的坐标为P(x,y)
由已知可得 $|MP|=\sqrt{2}|NP|$,即$\sqrt{{x^2}+{{(y-1)}^2}}=\sqrt{2}×\sqrt{{{(x-1)}^2}+{{(y-2)}^2}}$
整理 x2+y2-4x-6y+9=0,即(x-2)2+(y-3)2=4,其图形是以点(2,3)为圆心,2为半径的圆.…(4分)
(2)直线y=kx-1,即kx-y-1=0,圆心到此直线的距离小于半径$\frac{|2k-3-1|}{{\sqrt{{k^2}+1}}}<2$解得 $k>\frac{3}{4}$…(4分)
(3)设A(x1,kx1-1),B(x2,kx2-1),由$\overrightarrow{OA}•\overrightarrow{OB}=11$可得x1x2+(kx1-1)(kx2-1)=11,即(k2+1)x1x2-k(x1+x2)-10=0…①
又由$\left\{\begin{array}{l}y=kx-1\\{x^2}+{y^2}-4x-6y+9=0\end{array}\right.$消去y:(1+k2)x2-4(2k+1)x+16=0
由(2)知$k>\frac{3}{4}$∴${x_1}+{x_2}=\frac{4(2k+1)}{{1+{k^2}}}$,${x_1}{x_2}=\frac{16}{{1+{k^2}}}$…②
将②代入①可得$16-\frac{{8{k^2}+4k}}{{1+{k^2}}}-10=0$,解得k=1,或k=-3(不满足$k>\frac{3}{4}$)舍去,
∴当k=1时,$\overrightarrow{OA}•\overrightarrow{OB}=11$成立.…(4分)
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
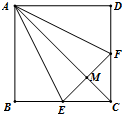 如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )
如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )| A. | PM⊥△AEF所在平面 | B. | AM⊥△PEF所在平面 | C. | PF⊥△AEF所在平面 | D. | AP⊥△PEF所在平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2-$\sqrt{7}$,1,3} | B. | {2-$\sqrt{7}$,1,3} | C. | {-3,-1,1,3} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -$\frac{8}{3}$ | C. | -$\frac{8}{3}$ 或8 | D. | 8或-$\frac{3}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com