
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
���� �����жϣ������ݺ����������ã��ڹ��캯��y=f��x��-x�����ж��䵥���Կɽ⣻�۹��캯��$y=\frac{f��x��}{x}$�������䵥�����ã������÷����������жϣ�
��� �⣺�����ݺ��������ʿ�֪������$f��x��={x}^{\frac{1}{2}}$�ڣ�1��+�ޣ���Ϊ�����������Ե�x��1ʱ��f��x����f��1��=1���ʢ���ȷ��
����g��x��=f��x��-x=${x}^{\frac{1}{2}}-x$����$g�䣨x��=\frac{1}{2\sqrt{x}}-1=\frac{1-2\sqrt{x}}{2\sqrt{x}}$�����Ե�x$�ʣ�0��\frac{1}{4}��$ʱg�䣨x����0����$x�ʣ�\frac{1}{4}��+�ޣ�$��g�䣨x����0����������x$�ʣ�0��\frac{1}{4}��$�ϵ�������$x�ʣ�\frac{1}{4}��+�ޣ�$�ϵݼ������Ե�$\frac{1}{4}��{x}_{1}��{x}_{2}$ʱ��g��x2����g��x1������f��x2��-x2��f��x1��-x1����f��x2��-f��x1����x2-x1���ʢڴ���
����h��x��=$\frac{f��x��}{x}={x}^{-\frac{1}{2}}$�����ݺ���������֪h��x��Ϊ���������ʵ�x1��x2ʱ����h��x1����h��x2������$\frac{f��{x}_{1}��}{{x}_{1}}$��$\frac{f��{x}_{2}��}{{x}_{2}}$����f��x1��x2��f��x2��x1���ʢ۴���Ҫ֤��$\frac{f��{x}_{1}��+f��{x}_{2}��}{2}$��$f��\frac{{x}_{1}+{x}_{2}}{2}��$����֤$\frac{\sqrt{{x}_{1}}+\sqrt{{x}_{2}}}{2}$��$\sqrt{\frac{{x}_{1}+{x}_{2}}{2}}$����ֻ��֤$\frac{{x}_{1}+{x}_{2}+2\sqrt{{x}_{1}{x}_{2}}}{4}$��$\frac{{x}_{1}+{x}_{2}}{2}$����ֻ��֤x1x2��$2\sqrt{{x}_{1}{x}_{2}}$����Ȼ�������ʢ���ȷ��
���ϣ���ȷ���Ϊ�٢ܣ�
��ѡ��B��
���� ����ע�⿼�麯�������Ե����ã��Ԣڢۣ����ò���ʽ�ص㹹�캯���ǽ���ؼ��������е��⣮


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2��b2 | B�� | ${��{\frac{1}{3}}��^a}��{��{\frac{1}{3}}��^b}$ | C�� | lg��a-b����1 | D�� | $\frac{b}{a}��1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4��14�� | B�� | ��6��6�� | C�� | ��3��18�� | D�� | ��10��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
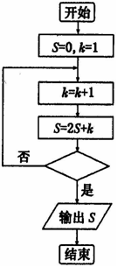
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com