
分析 (1)由圆C的方程求出圆心坐标和半径,设出M坐标,由$\overrightarrow{CM}$与$\overrightarrow{MP}$数量积等于0列式得M的轨迹方程;
(2)设M的轨迹的圆心为N,由|OP|=|OM|得到ON⊥PM.求出ON所在直线的斜率,由直线方程的点斜式得到PM所在直线方程,由点到直线的距离公式求出O到l的距离,再由弦心距、圆的半径及弦长间的关系求出PM的长度,代入三角形面积公式得答案;
(3)将直线与圆方程联立组成方程组,求出方程组的解得到两交点A与B的坐标,当圆面积最小时,弦AB为直径,利用两点间的距离公式求出|AB|的长,即为圆的直径,确定出圆的半径,利用线段中点坐标公式求出线段AB的中点坐标,即为圆心坐标,由圆心坐标和半径写出圆的标准方程即可.
解答 解:(1)圆C的方程可化为x2+(y-4)2=16,
所以圆心为C(0,4),半径为4.
设M(x,y),则$\overrightarrow{CM}$=(x,y-4),$\overrightarrow{MP}$=(2-x,2-y).
由题设知$\overrightarrow{CM}$•$\overrightarrow{MP}$=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.
由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
(2)由(1)可知M的轨迹是以点N(1,3)为圆心,$\sqrt{2}$为半径的圆.
由于|OP|=|OM|,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM.
因为ON的斜率为3,所以直线l的斜率为-$\frac{1}{3}$,
故l的方程为y=-$\frac{1}{3}$x+$\frac{8}{3}$.
又|OM|=|OP|=2 $\sqrt{2}$,O到直线l的距离为$\frac{4\sqrt{10}}{5}$,
故|PM|=$\frac{4\sqrt{10}}{5}$,所以△POM的面积为$\frac{16}{5}$.
(3)联立y=-$\frac{1}{3}$x+$\frac{8}{3}$与圆C:x2+y2-8y=0
得:5y2-28y+32=0,
解得:y1=4,y2=$\frac{8}{5}$,
当弦AB为直径时,圆面积最小,
则所求圆的直径为2R=|AB|=$\sqrt{1+9}•|4-\frac{8}{5}|$=$\frac{12\sqrt{10}}{5}$,
圆心为AB中点C(-$\frac{2}{5}$,$\frac{14}{5}$),
则所求面积最小的圆的方程是(x+$\frac{2}{5}$)2+(y-$\frac{14}{5}$)2=$\frac{72}{5}$.
点评 本题考查圆的轨迹方程的求法,训练了利用向量数量积判断两个向量的垂直关系,训练了点到直线的距离公式的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{5}$) | B. | (-$\sqrt{5}$,0) | C. | (-$\sqrt{13}$,0) | D. | (0,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
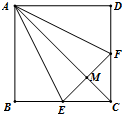 如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )
如图,正方形ABCD中,E,F分别是BC,CD的中点,M是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,则在四面体A-PEF中必有( )| A. | PM⊥△AEF所在平面 | B. | AM⊥△PEF所在平面 | C. | PF⊥△AEF所在平面 | D. | AP⊥△PEF所在平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2-$\sqrt{7}$,1,3} | B. | {2-$\sqrt{7}$,1,3} | C. | {-3,-1,1,3} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
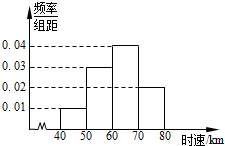 为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.
为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[40,60)内的汽车有80辆.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com