
【题目】设函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx)(k为常数,e=2.71828…是自然对数的底数).
+lnx)(k为常数,e=2.71828…是自然对数的底数).
(1)当k≤0时,求函数f(x)的单调区间;
(2)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
【答案】
(1)解: f(x)的定义域为(0,+∞),
∴f′(x)= ![]() ﹣k(
﹣k( ![]() ﹣
﹣ ![]() )
)
= ![]() (x>0),
(x>0),
当k≤0时,kx≤0,
∴ex﹣kx>0,
令f′(x)=0,则x=2,
∴当0<x<2时,f′(x)<0,f(x)单调递减;
当x>2时,f′(x)>0,f(x)单调递增,
∴f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞).
(2)解:由(1)知,k≤0时,函数f(x)在(0,2)内单调递减,
故f(x)在(0,2)内不存在极值点;
当k>0时,设函数g(x)=ex﹣kx,x∈(0,+∞).
∵g′(x)=ex﹣k=ex﹣elnk,
当0<k≤1时,
当x∈(0,2)时,g′(x)=ex﹣k>0,y=g(x)单调递增,
故f(x)在(0,2)内不存在两个极值点;
当k>1时,
得x∈(0,lnk)时,g′(x)<0,函数y=g(x)单调递减,
x∈(lnk,+∞)时,g′(x)>0,函数y=g(x)单调递增,
∴函数y=g(x)的最小值为g(lnk)=k(1﹣lnk)
函数f(x)在(0,2)内存在两个极值点
当且仅当 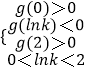
解得:e ![]()
综上所述,
函数f(x)在(0,2)内存在两个极值点时,k的取值范围为(e, ![]() )
)
【解析】(1)求出导函数,根据导函数的正负性,求出函数的单调区间;(2)函数f(x)在(0,2)内存在两个极值点,等价于它的导函数f′(x)在(0,2)内有两个不同的零点.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值(极值反映的是函数在某一点附近的大小情况)的相关知识才是答题的关键.
在这个区间单调递减),还要掌握函数的极值(极值反映的是函数在某一点附近的大小情况)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
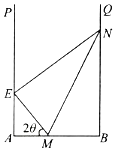
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为 ![]() ,在D上的概率为
,在D上的概率为 ![]() ;对落点在B上的来球,小明回球的落点在C上的概率为
;对落点在B上的来球,小明回球的落点在C上的概率为 ![]() ,在D上的概率为
,在D上的概率为 ![]() .假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响,求:
.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响,求: 
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,圆
,圆![]() :
:![]()
![]() (
(![]() ,且
,且![]() ).
).
(1)设![]() 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆![]() 与圆
与圆![]() 的一条切线,切点分别为
的一条切线,切点分别为![]() 、
、![]() ,使得
,使得![]() ,试求出所有满足条件的点
,试求出所有满足条件的点![]() 的坐标;
的坐标;
(2)若斜率为正数的直线![]() 平分圆
平分圆![]() ,求证:直线
,求证:直线![]() 与圆
与圆![]() 总相交.
总相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() , 平面
, 平面![]() ,Q是AD的中点,M是棱PC上的点,
,Q是AD的中点,M是棱PC上的点,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() ;
;
(2)若平面QMB与平面PDC所成的锐二面角的大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 、
、![]() 是同一平面上不共线的四点,若存在一组正实数
是同一平面上不共线的四点,若存在一组正实数![]() 、
、![]() 、
、![]() ,使得
,使得![]() ,则三个角
,则三个角![]() 、
、![]() 、
、![]() ( )
( )
A. 都是钝角B. 至少有两个钝角
C. 恰有两个钝角D. 至多有两个钝角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com