在等差数列{an}中，a1+a4+a7=39，a3+a6+a9=27，则数列{an}的前9项之和S9等于 ．
【答案】
分析：由等差数列的性质可求得a
4，=13，a
6=9，从而有a
4+a
6=22，由等差数列的前n项和公式即可求得答案．
解答：解：∵在等差数列{a
n}中，a
1+a
4+a
7=39，a
3+a
6+a
9=27，
∴a
4=13，a
6=9，
∴a
4+a
6=22，又a
4+a
6=a
1+a
9，，
∴数列{a
n}的前9项之和S
9=
=
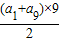
=99．
故答案为：99．
点评：本题考查等差数列的性质，掌握等差数列的性质与前n项和公式是解决问题的关键，属于中档题．
阅读快车系列答案
