
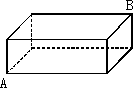
如图,长方体的长为12 cm,宽为6 cm,高为5 cm,一只蚂蚁沿该长方体的表面从点A向点B爬行.爬到点B时,蚂蚁最少爬了多远?
|
探究:先分析蚂蚁的爬行路线. (1)当蚂蚁首先沿朝向我们的这个面爬行时,下一步有可能沿上底面爬行,也有可能沿右侧面爬行.把上底面(或右侧面)展开,如图,此时,最短距离只可能是线段AB的长.由勾股定理得AB= 经比较知,此时最短路程为
(2)当蚂蚁首先沿下底面爬行时,下一步又有两种可能,即沿最里面的面或沿右侧面. 如图,得AB= 或AB= 经比较知,此时最短路程为
(3)当蚂蚁首先沿左侧面爬行时,下一步依然有两种可能,即沿最里面的面或沿上底面. 如图,得AB= 或AB= 经比较知,此时最短路程为 综上可知,蚂蚁最少爬了
|


科目:高中数学 来源: 题型:
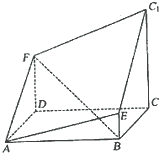 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
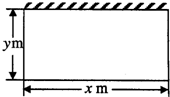 某单位计划建一长方体状的仓库,底面如图,高度为定值.仓库的后墙和底部不花钱,正面的造价为40元/m,两侧的造价为45元/m,顶部的造价为20元/m2.设仓库正面的长为x(m),两侧的长各为y(m).
某单位计划建一长方体状的仓库,底面如图,高度为定值.仓库的后墙和底部不花钱,正面的造价为40元/m,两侧的造价为45元/m,顶部的造价为20元/m2.设仓库正面的长为x(m),两侧的长各为y(m).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱AA1=2,P是侧棱CC1上的一点,CP=m(0<m<2).查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图,长方体 中
中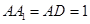 ,
,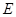 为
为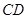 中点.
中点.
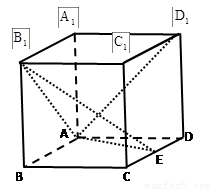
(1)求证: ;
;
(2)在棱上是否存在一点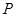 ,使得
,使得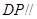 平面
平面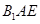 ?若存在,求
?若存在,求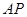 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(3)若二面角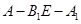 的大小为
的大小为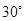 ,求
,求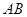 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com